Question

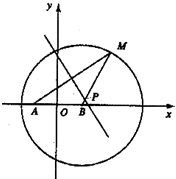（2003•崇文区一模）已知圆B方程（x-c）²+y²=4a²（a＞c＞0，a，c是常数），且A（-c，0），点M在圆B上运动，线段AM的垂直平分线交MB于点P．
（Ⅰ）判断点P的轨迹；
（Ⅱ）若满足题设的点P，使∠APB取其最大值

π

2

时，求点P的轨迹的离心率．

Answer 1

分析：（Ⅰ）由题意借助于等价转化得到∴|PA|+|PB|=|PM|+|PB|=|MB|=2a，由此可以判断P的轨迹；
（Ⅱ）在三角形APB中，利用余弦定理写出交APB的余弦值，配方后结合圆锥曲线的定义求出最小值，由最小值等于0解得点P鬼记得离心率．

解答：解：（I）连结AP，∴|PA|=|PM|，
∴|PA|+|PB|=|PM|+|PB|=|MB|=2a．
∵a＞c＞0，∴2a＞2c，且a、c是常数．
∴点P的轨迹是以A、B为焦点，长轴长为2a的椭圆；
（II）解：设|PA|=d₁，|PB|=d₂，由（I），得d₁+d₂=2a，|AB|=2c．
在△PAB中，由余弦定理，得
cos∠APB=

d 2 1 + d 2 2 -4c2

2d1d2

=

(d1+d2)2-2d1d2-4c2

2d1d2

=

4a2-4c2

2d1d2

-1
=

2(a2-c2)

d1d2

-1，
∵d1d2≤

(d1+d2)2

4

=a2（当且仅当d₁=d₂=a时，取等号）
∴cos∠APB≥

2(a2-c2)

a2

-1=1-

2c2

a2

．
∴cos∠APB的最小值为1-

2c2

a2

．
又0＜∠APB≤

π

2

，cos∠APB的最小值为0，
∴1-

2c2

a2

=0，

c

a

=

2

2

．
即当∠APB取其最大值

π

2

时，点P的轨迹的离心率e=

2

2

．

点评：本题考查了椭圆的简单几何性质，考查了椭圆的定义，训练了利用基本不等式求最值，与圆锥曲线有关的解三角形问题，经常结合圆锥曲线的定义及正余弦定理解题，此题是中高档题．