题目内容
已知圆C![]() ,D是
,D是![]() 轴上的动点,直线DA、DB分别切圆C于
轴上的动点,直线DA、DB分别切圆C于![]() 两点。
两点。
(1)如果![]() ,求直线CD的方程;
,求直线CD的方程;
(2)求动弦![]() 的中点的轨迹方程E;
的中点的轨迹方程E;
(3)直线![]() (
(![]() 为参数)与方程E交于P、Q两个不同的点,O为原点,设直线OP、OQ的斜率分别为
为参数)与方程E交于P、Q两个不同的点,O为原点,设直线OP、OQ的斜率分别为![]() ,试将
,试将![]() 表示成m的函数,并求其最小值。
表示成m的函数,并求其最小值。
解析:(1)设E为CD与AB的交点,由![]() ,可得
,可得

由![]() ∽
∽![]()
![]() ,
,![]()
所以点D坐标为![]() ∴直线MQ的方程是
∴直线MQ的方程是![]()
即![]() 或
或![]()
(2)设E![]() ,D(0,a)由点C,E,D在一条直线上,
,D(0,a)由点C,E,D在一条直线上,
得![]() ,∴
,∴![]() ①
①
由![]() ∽
∽![]()
![]() 即
即![]() ②
②
由①②消去![]() 得
得![]()
(3)设P、Q两点的坐标分别为![]() 和
和![]() ,联立
,联立![]() 和
和![]() 得
得![]() ,则
,则![]() ,
,
将韦达定理代入得
![]()
![]()
![]() 且又因为圆
且又因为圆![]() 的方程中
的方程中![]() 所以
所以![]() ,
,
![]() 时取得最小值,最小值为
时取得最小值,最小值为![]()

练习册系列答案
相关题目
 :
: ,
, 是
是 轴上的一点,
轴上的一点, 分别切圆
分别切圆 两点,且
两点,且 ,则直线
,则直线 的斜率为( )
的斜率为( ) C.1 D.
C.1 D.
 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 ,使得
,使得 ,则点
,则点 的横坐标
的横坐标 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
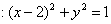 ,D是
,D是 轴上的动点,直线DA、DB分别切圆C于
轴上的动点,直线DA、DB分别切圆C于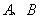 两点。
两点。 ,求直线CD的方程;
,求直线CD的方程;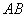 的中点的轨迹方程E;
的中点的轨迹方程E; (
( 为参数)与方程E交于P、Q两个不同的点,O为原点,设直线OP、OQ的斜率分别为
为参数)与方程E交于P、Q两个不同的点,O为原点,设直线OP、OQ的斜率分别为 ,试将
,试将 表示成m的函数,并求其最小值。
表示成m的函数,并求其最小值。