题目内容
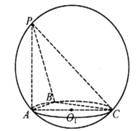
三棱锥P-ABC内接于球O,如果PA、PB、PC两两垂直且PA=PB=PC=a,则球心O到平面ABC的距离是______.
空间四个点P、A、B、C在同一球面上,PA、PB、PC两两垂直,且PA=PB=PC=a,
则PA、PB、PC可看作是正方体的一个顶点发出的三条棱,
所以过空间四个点P、A、B、C的球面即为棱长为a的正方体的外接球,
球的直径即是正方体的对角线,长为
a,
所以这个球面的半径
a,
球心O到平面ABC的距离为体对角线的
,
即球心O到平面ABC的距离为
a.
故答案为:
a.
则PA、PB、PC可看作是正方体的一个顶点发出的三条棱,
所以过空间四个点P、A、B、C的球面即为棱长为a的正方体的外接球,
球的直径即是正方体的对角线,长为
| 3 |
所以这个球面的半径
| 1 |
| 2 |
| 3 |
球心O到平面ABC的距离为体对角线的
| 1 |
| 6 |
即球心O到平面ABC的距离为
| ||
| 6 |
故答案为:
| ||
| 6 |

练习册系列答案
相关题目
 已知三棱锥P-ABC内接于球,三条侧棱两两垂直且长都为1,求球的表面积与体积.
已知三棱锥P-ABC内接于球,三条侧棱两两垂直且长都为1,求球的表面积与体积.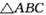 的外接圆为球O的小 圆
的外接圆为球O的小 圆 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是