题目内容
椭圆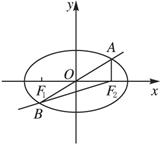
=1的左、右焦点分别为F1和F2，过中心O作直线与椭圆交于A、B两点，若△ABF2的面积为20，求直线AB的方程.
解：∵当AB⊥F1F2时，
·2·5≠20，?
∴AB与F1F2不能垂直.
∴可设直线AB的方程为y=kx，设A、B两点的坐标分别为（xa，ya）、（xb，yb）.?
由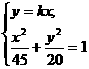
得（4+9k2）x2-180=0，
|xa-xb|=
×2.
∵S
=S
+S
=
|OF2|·|yb|+
|OF2|·|ya|?
=
×5（|yb|+|ya|）
=
|ya-yb|.
∵S
=20,
∴
|ya-yb|=20.?
∴|ya-yb|=8.
即|kxa-kxb|=8.?
把|xa-xb|=
×2代入上式并平方得4k2·
=64，∴k=±
.?
∴所求直线方程为y=±
x.
练习册系列答案
优等生题库系列答案
相关题目
+
=1的左、右焦点分别为F1、F2,点P在椭圆上.若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为（ ）
B.3 C.
D.
+
=1的左、右焦点分别为F1、F2，一直线过F1交椭圆于A、B两点，则△ABF2的周长为（ ）
+
=1的左、右焦点，A为椭圆上任一点，过焦点F1向∠F1AF2的外角平分线作垂线，垂足为D，则点D的轨迹方程是________________________________.
=1的左、右焦点是F1、F2，P是椭圆上的一点，线段PF1交y轴于点M，若|PF1|是|PF2|与?|F1F2|的等差中项，则
等于( )
+
=1的左、右焦点，A为椭圆上任一点，过焦点F1向∠F1AF2的外角平分线作垂线，垂足为D，则点D的轨迹方程是 ．