题目内容
 如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是线段AB中点.
如图,长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是线段AB中点.(1)证明:D1E⊥CE;
(2)求二面角D1-EC-D的大小的余弦值;
(3)求A点到平面CD1E的距离.
考点:点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)根据线面垂直的性质定理,证明CE⊥面D1DE即可证明:D1E⊥CE;
(2)建立坐标系,利用向量法即可求二面角D1-EC-D的大小的余弦值;
(3)根据点到平面的距离公式,即可求A点到平面CD1E的距离.
(2)建立坐标系,利用向量法即可求二面角D1-EC-D的大小的余弦值;
(3)根据点到平面的距离公式,即可求A点到平面CD1E的距离.
解答:
 解:(1)证明:DD1⊥面ABCD,CE?面ABCD
解:(1)证明:DD1⊥面ABCD,CE?面ABCD
所以,DD1⊥CE,
Rt△DAE中,AD=1,AE=1,
DE=
=
,
同理:CE=
,又CD=2,CD2=CE2+DE2,
DE⊥CE,
DE∩CE=E,
所以,CE⊥面D1DE,
又D1E?面D1EC,
所以,D1E⊥CE.
(2)设平面CD1E的法向量为
=(x,y,z),
由(1)得
=(1,1,-1),
=(1,-1,0)
•
=x+y-1=0,
•
=x-y=0
解得:x=y=
,即
=(
,
,1);
又平面CDE的法向量为
=(0,0,1),
∴cos<
,
>=
=
=
,
所以,二面角D1-EC-D的余弦值为
,
(3))由(1)(2)知
=(0,1,0),平面CD1E的法向量为
=(
,
,1)
故,A点到平面CD1E的距离为d=
=
=
.
 解:(1)证明:DD1⊥面ABCD,CE?面ABCD
解:(1)证明:DD1⊥面ABCD,CE?面ABCD所以,DD1⊥CE,
Rt△DAE中,AD=1,AE=1,
DE=
| AD2+AE2 |
| 2 |
同理:CE=
| 2 |
DE⊥CE,
DE∩CE=E,
所以,CE⊥面D1DE,
又D1E?面D1EC,
所以,D1E⊥CE.
(2)设平面CD1E的法向量为
| m |
由(1)得
| D1E |
| CE |
| m |
| D1E |
| m |
| CE |
解得:x=y=
| 1 |
| 2 |
| m |
| 1 |
| 2 |
| 1 |
| 2 |
又平面CDE的法向量为
| DD1 |
∴cos<
| m |
| DD1 |
| ||||
|
|
| 1 | ||||||
|
| ||
| 3 |
所以,二面角D1-EC-D的余弦值为
| ||
| 3 |
(3))由(1)(2)知
| AE |
| m |
| 1 |
| 2 |
| 1 |
| 2 |
故,A点到平面CD1E的距离为d=
|
| ||||
|
|
| ||||
|
| ||
| 6 |
点评:本题主要考查直线和平面垂直的性质,以及空间二面角和点到直线的距离的计算,利用向量法是解决本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )


| A、π | B、2π | C、4π | D、8π |
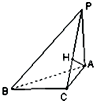 如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.
如图,已知△ABC中∠B=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为45°,AH⊥PC,垂足为H.求二面角A-PB-C的正弦值.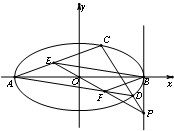 如图,在平面直角坐标系xOy中,A、B分别是椭圆:
如图,在平面直角坐标系xOy中,A、B分别是椭圆: