题目内容
在△ABC中,若已知三边为连续正整数,最大角为钝角.
(1)求最大角的余弦值;
(2)求以此最大角为内角,夹此角的两边之和为4的平行四边形的最大面积.
解 (1)设这三个数为n,n+1,n+2,最大角为θ,
则cos θ= <0,
<0,
化简得:n2-2n-3<0⇒-1<n<3.
∵n∈N*且n+(n+1)>n+2,∴n=2.
∴cos θ= =-
=- .
.
(2)设此平行四边形的一边长为a,则夹θ角的另一边长为4-a,平行四边形的面积为:
S=a(4-a)·sin θ=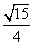 (4a-a2)=
(4a-a2)=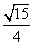 [-(a-2)2+4]≤
[-(a-2)2+4]≤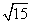 .
.
当且仅当a=2时,Smax=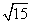 .
.

练习册系列答案
相关题目
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如表所示:
| 产品消耗量资源 | 甲产品 | ||
| (每吨) | 乙产品 | ||
| (每吨) | 资源限额 | ||
| (每天) | |||
| 煤(t) | 9 | 4 | 360 |
| 电力(kw· h) | 4 | 5 | 200 |
| 劳动力(个) | 3 | 10 | 300 |
| 利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨时,获得利润总额最大?
 <β<π,tan
<β<π,tan =
=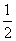 ,cos(β-α)=
,cos(β-α)=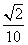 .
. )a<(
)a<( >1
>1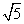 ,b=
,b=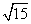 ,A=30°,则c等于( )
,A=30°,则c等于( )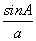 =
=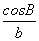 =
=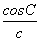 ,则△ABC是( )
,则△ABC是( )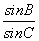 的值为( )
的值为( )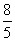 B.
B.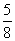 C.
C.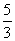 D.
D.
 若
若 ,则
,则 ( )
( )