题目内容
关于函数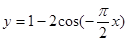 的叙述,正确的是( )
的叙述,正确的是( )
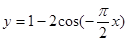 的叙述,正确的是( )
的叙述,正确的是( )A.在 上递减偶函数 上递减偶函数 | B.在(0,1)上递减偶函数 |
C.在 上递增奇函数 上递增奇函数 | D.在(0, 1)上递增偶函数 |
D
试题分析:

 是偶函数,当
是偶函数,当 时
时 是增函数
是增函数点评:函数的奇偶性单调性是考察最多的性质

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
题目内容
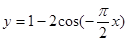 的叙述,正确的是( )
的叙述,正确的是( )A.在 上递减偶函数 上递减偶函数 | B.在(0,1)上递减偶函数 |
C.在 上递增奇函数 上递增奇函数 | D.在(0, 1)上递增偶函数 |

 是偶函数,当
是偶函数,当 时
时 是增函数
是增函数
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案