题目内容
设函数f(x)=sin(2x+φ),(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
(Ⅰ)求φ;
(Ⅱ)求函数y=f(x)的单增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图像不相切.

(Ⅰ)求φ;
(Ⅱ)求函数y=f(x)的单增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图像不相切.
(Ⅰ)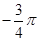
(Ⅱ)单调增区间为[kπ+ kπ+
kπ+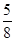 π],k∈Z,
π],k∈Z,
(Ⅲ)见解析
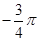
(Ⅱ)单调增区间为[kπ+
 kπ+
kπ+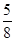 π],k∈Z,
π],k∈Z,(Ⅲ)见解析
【错解分析】由对称轴是x=
 ,可知2×
,可知2× +φ使f(x)取最值,即
+φ使f(x)取最值,即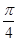 +φ=kπ+
+φ=kπ+ .(k∈Z),从而可求φ;由sinx的单增区间可求f(x)=sin(2x+φ)的单增区间.由|f′(x)|=|2cos(2x+φ)|≤2,直线5x-2y+c=0的斜率为
.(k∈Z),从而可求φ;由sinx的单增区间可求f(x)=sin(2x+φ)的单增区间.由|f′(x)|=|2cos(2x+φ)|≤2,直线5x-2y+c=0的斜率为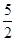 >2说明直线和f(x)的图象不能相切.
>2说明直线和f(x)的图象不能相切.【正解】(Ⅰ)解法1:因为x=
 是函数y=f(x)的图像的对称轴,
是函数y=f(x)的图像的对称轴,所以sin(2·
 +φ)=±1, 则有
+φ)=±1, 则有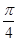 +φ=kπ+
+φ=kπ+ ,k∈Z.
,k∈Z. 因为-π<φ<0, 所以φ=-
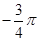
解法2:函数y="sin" 2x图像的对称轴为x=
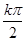 +
+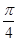 ,k∈Z.
,k∈Z.y=sin(2x+φ)的图像由y="sin" 2x的图像向左平移
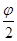 得到,
得到,所以有
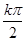 +
+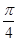 -
-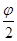 =
= k∈Z.
k∈Z.∵-π<φ<0,∴φ=
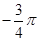 .
.解法3:因为x=
 是函数y=f(x)的图像的对称轴. 所以f(
是函数y=f(x)的图像的对称轴. 所以f( -x)=f(
-x)=f( +x).
+x).即sin[2(
 -x)+φ]=sin[2(
-x)+φ]=sin[2( +x)+φ],
+x)+φ],于是有2(
 -x)+φ=2kπ+2(
-x)+φ=2kπ+2( +x)+φ(舍去),
+x)+φ(舍去),或[2(
 -x)+φ]+[2(
-x)+φ]+[2( +x)+φ]=2kπ+π.
+x)+φ]=2kπ+π. 因为-π<φ<0,∴φ=
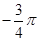
(Ⅱ)解法1:由(Ⅰ)知φ=-
 π,因此y=sin(2x-
π,因此y=sin(2x- π),
π), 由题意得2kπ-
 ≤2x-
≤2x- π≤2kπ+
π≤2kπ+ ,(k∈Z),
,(k∈Z),所以函数y=sin(2x-
 π)的单调增区间为[kπ+
π)的单调增区间为[kπ+ kπ+
kπ+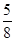 π],k∈Z,
π],k∈Z,解法2:由y′=2cos(2x-
 π)≥0可得,2kπ-
π)≥0可得,2kπ- ≤2x-
≤2x- π≤2kπ+
π≤2kπ+ k∈Z,
k∈Z,所以函数y=sin(2x-
 π)的单调增区间为[kπ+
π)的单调增区间为[kπ+ ,kπ+
,kπ+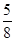 π] k∈Z,
π] k∈Z,(Ⅲ)解法1:因为|y′|=|[sin(2x-
 π)]′|=|2cos(2x-
π)]′|=|2cos(2x- π)|≤2,
π)|≤2,所以曲线y=f(x)的切线斜率取值范围为[-2,2],而直线5x-2y+c=0的斜率
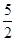 >2,
>2,所以直线5x-2y+c=0与函数y=sin(2x-
 π)的图象不相切.
π)的图象不相切.解法2:令F(x)=sin(2x-
 π)-
π)-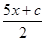 ,
, 则F′(x)=2cos(2x-
 π)-
π)-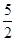 ,
,∵-1≤cos(2x-
 π)≤1,F′(x)≠0.
π)≤1,F′(x)≠0. 则直线5x-2y+c=0与函数y=sin(2x-
 π)的图像不相切.
π)的图像不相切.【点评】本题第(Ⅰ)(Ⅱ)问是三角函数中最基本的问题,第(Ⅲ)问是考查一般函数在某点导数的几何意义,涉及的都是一些基本的概念,也是每个同学应该掌握的.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 ,则点
,则点 位于( )
位于( )
 的最小正周期; 2)求函数
的最小正周期; 2)求函数 上的对称轴方程与零点.
上的对称轴方程与零点. 的值域是________________________.
的值域是________________________.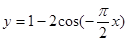 的叙述,正确的是( )
的叙述,正确的是( ) 上递减偶函数
上递减偶函数 中,
中, 分别是角
分别是角 ,
, ,
, 的对边,且
的对边,且 .
. 求
求 的单调增区间;
的单调增区间; ,求
,求 的最小正周期为
的最小正周期为 ,当
,当 时,函数
时,函数 的最小值为0。
的最小值为0。 ,若
,若 的值。
的值。 ,其中
,其中
 在区间
在区间 上的值域;
上的值域; 中,
中, .
. ,
, 分别是角
分别是角 的对边,
的对边,  ,且
,且
 ,求边
,求边 为锐角,若
为锐角,若 ,则
,则 的值为 .
的值为 .