题目内容
9.做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )| A. | $\frac{a}{b}$ | B. | $\frac{a^2}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{b^2}{a}$ |
分析 设锅炉的高h与底面直径d的比为k=$\frac{h}{d}$,运用圆柱的表面积公式和体积公式,结合导数,求得极值点且为最值点,即可得到.
解答 解:设锅炉的高h与底面直径d的比为k=$\frac{h}{d}$,
由V=$\frac{π{d}^{2}}{4}$h=$\frac{π{d}^{2}}{4}$•kd=$\frac{π}{4}$kd3,
可得d=$\root{3}{\frac{4V}{kπ}}$,h=kd=$\root{3}{\frac{4v{k}^{2}}{π}}$,
设造价为y,则y=2π•($\frac{d}{2}$)2•a+πdh•b,
则y′=$\frac{πa}{2}•\root{3}{\frac{16{V}^{2}}{{π}^{2}}}•(-\frac{2}{3}){k}^{-\frac{5}{3}}$+$πb•\root{3}{\frac{16{V}^{2}}{{π}^{2}}}•\frac{1}{3}{k}^{-\frac{2}{3}}$
令y′=0,解得k=$\frac{a}{b}$,可得此时y取得最小值.
故当造价最低时,锅炉的高与底面直径的比为$\frac{a}{b}$.
故选C.
点评 本题考查函数在实际问题中的运用,考查导数的运用:求最值,同时考查圆柱的表面积和体积的运用,属于中档题.

练习册系列答案
相关题目
19.为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
(1)根据以上数据完成2×2列联表;
(2)是否有90%的把握认为“睡眠时间与性别有关”?
附临界参考表
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$.
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 女生人数 | 2 | 4 | 8 | 4 | 2 |
| 男生人数 | 1 | 5 | 6 | 5 | 3 |
(2)是否有90%的把握认为“睡眠时间与性别有关”?
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | 12 | 8 | 20 |
| 女生 | 14 | 6 | 20 |
| 合计 | 26 | 14 | 40 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18.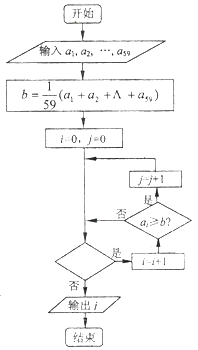 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
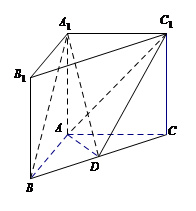 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.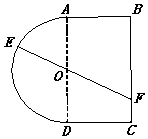 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.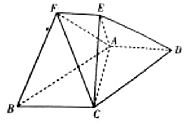 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.