题目内容
四点O,A,B,C共面,若
+
+2
=
,则△AOC的面积与△ABC的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,延长CO到点D,使得OD=2OC.以OA,OB为邻边作平行四边形OAEB.由于
+
=2
.
+
+2
=
,可得点O是CD的中点.即可得出.
| OA |
| OB |
| OD |
| OA |
| OB |
| OC |
| 0 |
解答:
解:如图所示,延长CO到点D,使得OD=2OC.以OA,OB为邻边作平行四边形OAEB.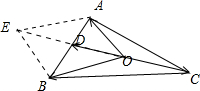
则
+
=2
.
∵
+
+2
=
,
∴2
+2
=
.
∴点O是CD的中点.
∴△AOC的面积与△ABC的面积之比=
.
故选:D.

则
| OA |
| OB |
| OD |
∵
| OA |
| OB |
| OC |
| 0 |
∴2
| OD |
| OC |
| 0 |
∴点O是CD的中点.
∴△AOC的面积与△ABC的面积之比=
| 1 |
| 4 |
故选:D.
点评:本题考查了向量的平行四边形法则、三角形的面积之比等基础知识与基本技能方法,考查了推理能力,考查了数形结合的能力,属于中档题.

练习册系列答案
相关题目
下列各组角中,终边相同的是( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知全集U=R,集合M={x|x≥1},N={x|
≥0},则M∩N=( )
| x+1 |
| x-2 |
| A、{x|x≥2} |
| B、{x|x>2} |
| C、{x|1≤x≤2} |
| D、{x|1≤x<2} |
若2x+3y+5z=29,则函数μ=
+
+
的最大值为( )
| 2x+1 |
| 3y+4 |
| 5z+6 |
A、
| ||
B、2
| ||
C、2
| ||
D、
|
若△ABC的内角A、B、C所对的边a、b、c,若角A、B、C依次成等差数列,且(a+c)2=12+b2,则△ABC的面积为( )
A、6-3
| ||
B、6
| ||
C、2
| ||
D、
|
设有算法如图所示,如果输入A=144,B=39,则输出的结果是( )


| A、144 | B、3 | C、0 | D、12 |
已知O是坐标原点,点A(2,m)、B(m+1,3),若
∥
,则实数m的值为( )
| OA |
| OB |
| A、2 | ||
| B、-3 | ||
| C、2或-3 | ||
D、-
|
用0,3,5,6,7,8组成无重复数字的五位数,其中能被3整除的五位数有( )
| A、96个 | B、48个 |
| C、192个 | D、240个 |