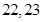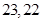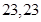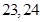题目内容
在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.如果a,b,c成等差数列,∠B=30°,△ABC的面积为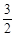 ,那么b=( ).
,那么b=( ).
A.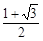 | B.1+ | C.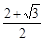 | D.2+ |
B
解析试题分析:根据等差中项的性质可知2b=a+c.平方后整理得a2+c2=4b2-2ac.利用三角形面积求得ac的值,进而把a2+c2=4b2-2ac.代入余弦定理求得b的值.:∵a,b,c成等差数列,∴2b=a+c.平方得a2+c2=4b2-2ac.又△ABC的面积为 ,且∠B=30°,故由S△=
,且∠B=30°,故由S△=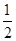 acsinB=
acsinB=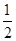 ac•sin30°=
ac•sin30°=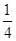 ac=
ac= ,得ac=6,∴a2+c2=4b2-12.由余弦定理
,得ac=6,∴a2+c2=4b2-12.由余弦定理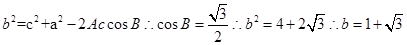 ,故选B
,故选B
考点:正弦定理,余弦定理
点评:本题主要考查了解三角形的问题.解题过程中常需要正弦定理,余弦定理,三角形面积公式以及勾股定理等知识.

练习册系列答案
相关题目
已知等差数列 的前三项依次为
的前三项依次为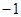 ,
, ,
,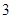 ,则此数列的通项公式为( )
,则此数列的通项公式为( )
A.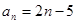 | B.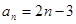 | C.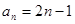 | D.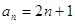 |
等差数列 的前
的前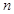 项的和为
项的和为 ,且
,且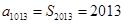 ,则
,则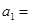 ( )
( )
| A. 2012 | B.2012 | C. 2011 | D.2011 |
等差数列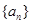 :1,4,7,……中,当
:1,4,7,……中,当 时,序号
时,序号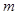 等于
等于
| A.99 | B.100 | C.96 | D.101 |
若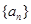 是等差数列,首项公差
是等差数列,首项公差 ,
,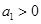 ,且
,且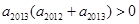 ,则使数列
,则使数列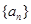 的前n项和
的前n项和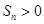 成立的最大自然数n是 ( )
成立的最大自然数n是 ( )
| A.4027 | B.4026 | C.4025 | D.4024 |
若数列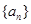 是等差数列,且
是等差数列,且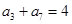 ,则数列
,则数列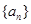 的前
的前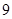 项和
项和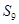 等于
等于
A.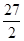 | B.18 | C.27 | D.36 |
等差数列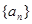 中,已知前
中,已知前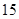 项的和
项的和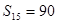 ,则
,则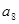 等于( )
等于( )
A.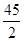 | B.12 | C.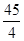 | D.6 |
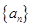 中,若a
中,若a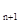 - a
- a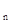
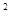 + a
+ a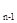 =0(n≥2),则S
=0(n≥2),则S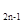 -4n=( )
-4n=( )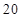 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为 的等差数列
的等差数列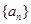 ,若
,若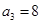 且前
且前 项和
项和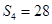 ,则此样本的平均数和中位数分别是
,则此样本的平均数和中位数分别是