题目内容
7.已知函数f(x)=ex-ax(1)若函数f(x)在x=1处取得极值,求函数y=f(x)在点(0,f(0))处的切线方程;
(2)当x≥0,f(x)-f(-x)≥0恒成立,求a的最大值;
(3)当a=1,解关于x的不等式:$\left\{\begin{array}{l}{f(x)≤f(1)}\\{f(-x)≤f(1)}\end{array}\right.$.
分析 (1)由函数f(x)在x=1处取得极值知a=e,切点(0,1)处的切线方程由点斜式可以直接给出.
(2)分离参数,构造新函数,由不等式的性质可得出a的范围.
(3)由函数的对称性得知两个图形重合时取之间值.
解答 解:(1)∵函数f(x)=ex-ax
∴f′(x)=ex-a
∵函数f(x)在x=1处取得极值
∴f′(1)=0
∴a=e
∴f′(x)=ex-e
k=f′(0)=1-e
f(0)=1
∴函数y=f(x)在点(0,1)处的切线方程为y-1=(1-e)x.
(2)当x≥0,f(x)-f(-x)=ex-e-x-2ax≥0恒成立,
x=0时,0=0,上式成立.
x>0时,原式等价于a≤$\frac{{e}^{x}-{e}^{-x}}{2x}$恒成立.
令g(x)=$\frac{{e}^{x}-{e}^{-x}}{2x}$,只需a≤g(x)的最小值即可.
∵g′(x)=$\frac{2x({e}^{x}+{e}^{-x})-2({e}^{x}-{e}^{-x})}{(2x)^{2}}$
令φ(x)=x(ex+e-x)-ex+e-x
则φ′(x)=x(ex-e-x)
∵x≥0
∴φ′(x)≥0
∴φ(x)在x≥0是单调递增的,φ(x)的最小值为φ(0)=0
∴g′(x)≥0在x>0恒成立
∴g(x)在x>0上单调递增恒成立
g(x)的最小值大于0
∴a≤0
(3)∵f(x)与f(-x)关于y轴对称.
f(-1)=e-1+1=$\frac{1}{e}$+1<e-1
且f(x)在(-∞,0)单调递减,在(0,+∞)上单调递增
由对称性知,-1≤x≤1
点评 本题考查函数的导函数与函数的性质.而第三问比较巧妙的利用函数的对称性.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
17.已知抛物线C:x2=4y的焦点为F,准线为l,P是l上一点,Q是直线PF与抛物线C的一个交点,若$\overrightarrow{PF}=4\overrightarrow{QF}$,则|QF|=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |
18.一个样本的数据在60左右波动,各个数据都减去60后得到一组新数据,算得其平均数是6,则这个样本的平均数是( )
| A. | 6.6 | B. | 6 | C. | 66 | D. | 60 |
19.已知点M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),若椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,则a的取值范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [$\sqrt{2}$,+∞) |
16.已知函数$f(x)=2\sqrt{3}sin(3ωx+\frac{π}{3})\;(ω>0)$,若f(x+θ)是周期为2π的偶函数,则θ的一个可能值是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{7}{6}π$ | C. | π | D. | $\frac{5}{6}π$ |
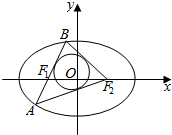 如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.