题目内容
4.函数f(x)=$\frac{(x+1)(x+a)}{x^3}$为奇函数,则a=-1.分析 由题意可得f(-x)=-f(x),由此求得a的值.
解答 解:∵函数f(x)=$\frac{(x+1)(x+a)}{x^3}$为奇函数,
故有f(-x)=$\frac{(-x+1)(-x+a)}{{(-x)}^{3}}$=$\frac{(x-1)(x-a)}{{-x}^{3}}$=-f(x)=-$\frac{(x+1)(x+a)}{{x}^{3}}$,
即 (x-1)(x-a)=(x+1)(x+a),
即x2-(a+1)x+a=x2+(a+1)x+a,∴a+1=0,∴a=-1,
故答案为:-1.
点评 本题主要考查奇函数的性质,属于基础题.

练习册系列答案
相关题目
12.如图,α-MN-β为120°,O∈MN,a∈β,B∈α.∠BON=∠AOM=45°,$OA=OB=\sqrt{2}$,则AB=( )
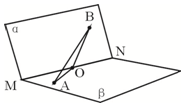

| A. | $\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
9.设函数f(x)=log2x-2-x,g(x)=log${\;}_{\frac{1}{2}}$x-2x的零点分别为x1,x2,则下列结论正确的是( )
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<2 | D. | x1x2≥2 |
16.直线$\sqrt{3}$x+y+1=0的倾斜角为( )
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
14.已知$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,1),$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则cosθ=( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{15}}{5}$ |
 如图,在△ABC中,D,E分别为BC,AB的中点,F为AD的中点.
如图,在△ABC中,D,E分别为BC,AB的中点,F为AD的中点.