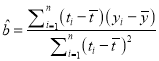题目内容
【题目】已知椭圆系方程![]() :
: ![]() (
(![]() ,
, ![]() ),
), ![]() 是椭圆
是椭圆![]() 的焦点,
的焦点, ![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的离心率并求出
的离心率并求出![]() 的方程;
的方程;
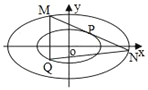
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() 且与椭圆
且与椭圆![]() 相切的直线
相切的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,求证:
,求证: ![]() 的面积为定值,并求出这个定值.
的面积为定值,并求出这个定值.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由椭圆![]() 的方程为:
的方程为: ![]() ,由
,由![]() ,∴
,∴![]() , 可得
, 可得![]() 的值,得到椭圆方程;
的值,得到椭圆方程;
(2)由距离公式得到点![]() 到直线
到直线![]() 的距离
的距离![]() ,由弦长公式得到
,由弦长公式得到![]() 的面积为
的面积为![]() ,即可得到面积为定值,得到证明.
,即可得到面积为定值,得到证明.
试题解析:
(1)椭圆![]() 的方程为:
的方程为: ![]() :
: ![]() 即:
即: ![]()
∵![]() .∴
.∴![]() ,又
,又![]()
![]()
![]() 即:
即: ![]() 又
又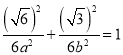
![]() ,
,![]() ∴椭圆
∴椭圆![]() 的方程为:
的方程为: ![]()
∴![]() ,∴
,∴ ![]() ∴椭圆
∴椭圆![]() 的方程为:
的方程为:![]() ;
; 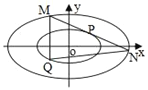
(2)解法(一):设![]() ,则
,则![]()
当直线l斜率存在时,设l为: ![]() ,
,
则![]() ,由
,由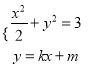 联立得:
联立得: ![]()
由![]() 得
得![]()
![]() 到直线
到直线![]() 的距离
的距离![]()
同理,由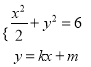 联立得:
联立得: ![]()
![]() ,
, ![]()
![]()
![]()
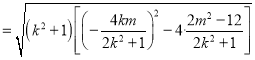
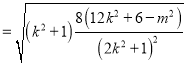
![]()
![]()
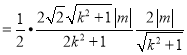
![]()
![]()
![]()
当直线l斜率不存在时,易知![]() ,
, ![]() 的面积为定值
的面积为定值![]()
解法(二):设![]() ,由(1)得
,由(1)得![]() 为:
为: ![]() ,
,
∴过![]() 且与椭圆
且与椭圆![]() 相切的直线l:
相切的直线l: ![]() .且
.且![]()
点![]() 关于原点对称点
关于原点对称点![]() ,点
,点![]() 到直线l的距离
到直线l的距离
设![]() ,
, ![]()
由![]() 得
得![]()
![]()
![]() ,
, ![]() ,∴
,∴ 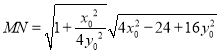
![]()
∴![]() 的面积为
的面积为
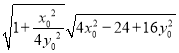
![]() (定值)
(定值)
当![]() 时,易知
时,易知![]() ,
,
综上: ![]() 的面积为定值
的面积为定值![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.