题目内容
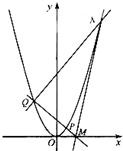
过抛物线C:x2=4y的焦点F作直线l,交C于A,B两点.若F恰好为线段AB的三等分点,则直线l的斜率k=
或-
或-
.
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
分析:由抛物线C:x2=4y得焦点F(0,1).设A(x1,
),B(x2,
).由于F恰好为线段AB的三等分点,利用向量可得
=2
,或
=
.即可得到横坐标之间的关系.另一方面可得直线l的方程为y=kx+1,与抛物线的方程联立即可得到根与系数的关系,即可解出k的值.
| ||
| 4 |
| ||
| 4 |
| AF |
| FB |
| AF |
| 1 |
| 2 |
| FB |
解答:解:由抛物线C:x2=4y得焦点F(0,1).
设A(x1,
),B(x2,
).∵F恰好为线段AB的三等分点,∴
=2
,或
=
.
①当
=2
时,得-x1=2x2,由直线l的方程为y=kx+1,与抛物线方程联立得
,消去y得到x2-4kx-4=0,得到x1+x2=4k,x1x2=-4.
联立
,解得k=±
.
②当
=
时,同上,k=±
.
故答案为±
.
设A(x1,
| ||
| 4 |
| ||
| 4 |
| AF |
| FB |
| AF |
| 1 |
| 2 |
| FB |
①当
| AF |
| FB |
|
联立
|
| ||
| 4 |
②当
| AF |
| 1 |
| 2 |
| FB |
| ||
| 4 |
故答案为±
| ||
| 4 |
点评:本题综合考查了抛物线的标准方程及其性质、直线与抛物线的相交关系、根与系数的关系、向量的共线、三等分点等基础知识与基本技能,考查了推理能力和计算能力.

练习册系列答案
相关题目
 已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为
已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为 已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为
已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为