题目内容
已知A、B两点在抛物线C:x2=4y上,点M(0,4)满足| MA |
| BM |
(1)求证:
| OA |
| OB |
(2)设抛物线C过A、B两点的切线交于点N.
①求证:点N在一条定直线上;
②设4≤λ≤9,求直线MN在x轴上截距的取值范围.
分析:先设A,B的坐标和直线AB的方程,再联立直线与抛物线方程消去y得到关于x的一元二次方程得到两根之和与两根之积.
(1)根据向量的数量积运算表示出
•
,然后将所求的两根之和与两根之积代入即可得到:
•
=0,进而的得证.
(2)①先表示出过点A的切线和过点B的切线,然后两直线联立可求出点N的坐标,即可得到点N在定直线y=-4上.
②根据
=λ
可知(x1,y1-4)=λ(-x2,4-y2),进而可联立方程可求得k2的表达式,进而求得k2的范围,最后根据直线MN在x轴的截距为k,进而可得答案.
(1)根据向量的数量积运算表示出
| OA |
| OB |
| OA |
| OB |
(2)①先表示出过点A的切线和过点B的切线,然后两直线联立可求出点N的坐标,即可得到点N在定直线y=-4上.
②根据
| MA |
| BM |
解答:解:设A(x1,y1),B(x2,y2),lAB:y=kx+4与x2=4y联立得x2-4kx-16=0,
△=(-4k)2-4(-16)=16k2+64>0,
x1+x2=4k,x1x2=-16,
(1)证明:
•
=x1x2+y1y2=x1x2+(kx1+4)(kx2+4)
=(1+k2)x1x2+4k(x1+x2)+16
=(1+k2)(-16)+4k(4k)+16=0,
∴
⊥
.
(2)①证明:过点A的切线:
y=
x1(x-x1)+y1=
x1x-
x12,①
过点B的切线:y=
x2x-
x22,②
联立①②结合(1)的结论得点N(
,-4),
所以点N在定直线y=-4上.
②∵
=λ
,∴(x1,y1-4)=λ(-x2,4-y2),
联立可得
k2=
=
=λ+
-2,4≤λ≤9,
∴
≤k2≤
.
直线MN:y=
x+4在x轴的截距为k,
∴直线MN在x轴上截距的取值范围是
[-
,-
]∪[
,
].
△=(-4k)2-4(-16)=16k2+64>0,
x1+x2=4k,x1x2=-16,
(1)证明:
| OA |
| OB |
=x1x2+y1y2=x1x2+(kx1+4)(kx2+4)
=(1+k2)x1x2+4k(x1+x2)+16
=(1+k2)(-16)+4k(4k)+16=0,
∴
| OA |
| OB |
(2)①证明:过点A的切线:
y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
过点B的切线:y=
| 1 |
| 2 |
| 1 |
| 4 |
联立①②结合(1)的结论得点N(
| x1+x2 |
| 2 |
所以点N在定直线y=-4上.
②∵
| MA |
| BM |
联立可得
|
k2=
| (1-λ)2 |
| λ |
| λ2-2λ+1 |
| λ |
| 1 |
| λ |
∴
| 9 |
| 4 |
| 64 |
| 9 |
直线MN:y=
| -8 |
| 2k |
∴直线MN在x轴上截距的取值范围是
[-
| 8 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 8 |
| 3 |
点评:本题主要考查了抛物线的应用.涉及了抛物线的性质,向量的计算,不等式等知识.

练习册系列答案
相关题目
 ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点. 时,求k的值.
时,求k的值. ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.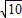 时,求k的值.
时,求k的值. ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点. 时,求k的值.
时,求k的值.