Question

已知抛物线C：x²=2py（p＞0）上一点A（m，4）到其焦点的距离为

17

4

．
（I）求p于m的值；
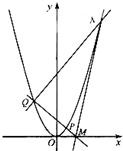
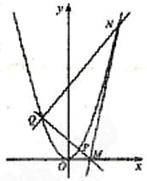
（Ⅱ）设抛物线C上一点p的横坐标为t（t＞0），过p的直线交C于另一点Q，交x轴于M点，过点Q作PQ的垂线交C于另一点N．若MN是C的切线，求t的最小值．

Answer 1

分析：（1）由抛物线方程得其准线方程，进而根据抛物线定义可知点A（m，4）到焦点的距离等于它到准线的距离，求得p，则抛物线方程可得，把点A代入抛物线方程即可求得m．
（2）由题意知，过点P（t，t²）的直线PQ斜率存在且不为0，设其为k．则根据点斜式可知直线PQ的直线方程与抛物线方程联立消去y，解得方程的根，根据QN⊥QP，进而可知NQ的直线方程与抛物线方程联立，解得方程的根．进而可求得直线NM的斜率，依据MN是抛物线的切线，则可求得物线在点N处切线斜率进而可建立等式．根据判别式大于等于0求得t的范围．

解答：解：（Ⅰ）由抛物线方程得其准线方程：
y=-

p

2

，根据抛物线定义
点A（m，4）到焦点的距离等于它到准线的距离，
即4+

p

2

=

17

4

，解得p=

1

2

∴抛物线方程为：x²=y，将A（m，4）代入抛物线方程，解得m=±2
（Ⅱ）由题意知，过点P（t，t²）的直线PQ斜率存在且不为0，设其为k．
则l_PQ：y-t²=k（x-t），
当y=0，x=

-t2+kt

k

，
则M(

-t2+kt

k

，0)．
联立方程

y-t2=k(x-t) x2=y

，
整理得：x²-kx+t（k-t）=0
即：（x-t）[x-（k-t）]=0，
解得x=t，或x=k-t∴Q（k-t，（k-t）²），
而QN⊥QP，∴直线NQ斜率为-

1

k

∴lNQ：y-(k-t)2=-

1

k

[x-(k-t)]，
联立方程

y-(k-t)2=- 1 k [x-(k-t)] x2=y

整理得：x2+

1

k

x-

1

k

(k-t)-(k-t)2=0，
即：kx²+x-（k-t）[k（k-t）+1]=0[kx+k（k-t）+1][x-（k-t）]=0，
解得：x=-

k(k-t)+1

k

，
或x=k-t∴N(-

k(k-t)+1

k

，

[k(k-t)+1]2

k2

)，
∴KNM=

[k(k-t)+1]2 k2

- k(k-t)+1 k - -t2+kt k

=

(k2-kt+1)2

k(t2-k2-1)

而抛物线在点N处切线斜率：k切=y′

|	x= k(k-t)+1 k

=-

k(k-t)+1

k

∵MN是抛物线的切线，
∴

(k2-kt+1)2

k(t2-k2-1)

=

-2k(k-t)-2

k

，
整理得k²+tk+1-2t²=0
∵△=t²-4（1-2t²）≥0，
解得t≤-

2

3

（舍去），或t≥

2

3

，∴tmin=

2

3

点评：本题主要考查了抛物线的简单性质．考查了学生对直线与抛物线的关系，直线的斜率等问题综合把握．