题目内容
已知△ABC的内角A、B、C成等差数列,且A、B、C所对的边分别为a、b、c,则下列命题中正确的有________(把所有正确的命题序号都填上).
①B=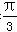 ;
;
②若a、b、c成等比数列,则△ABC为等边三角形;
③若a=2c,则△ABC为锐角三角形;
④若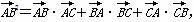 则3A=C;
则3A=C;
⑤若tan A+tan C+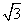 >0,则△ABC为钝角三角形.
>0,则△ABC为钝角三角形.
①②④
[解析]∵内角A、B、C成等差数列,∴A+C=2B.
又A+B+C=π.∴B=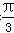 ,故①正确;
,故①正确;
对于②,由余弦定理得b2=a2+c2-2ac·cos B=a2+c2-ac.
又b2=ac,∴a2+c2-ac=ac,即(a-c)2=0,∴a=c,又B=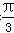 ,∴△ABC为等边三角形;
,∴△ABC为等边三角形;
对于③,∵b2=a2+c2-2accos B=4c2+c2 -2c2=3c2,
-2c2=3c2,
∴b=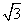 c,此时满足a2=b2+c2,说明△ABC是直角三角形;
c,此时满足a2=b2+c2,说明△ABC是直角三角形;
对于④,c2=bccos A+accos B+abcos C=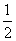 ac+b(ccos A+acos C)
ac+b(ccos A+acos C)
=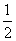 ac+b2=
ac+b2=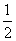 ac+a2+c2-ac,化简得c=2a,又b2=a2+c2-ac=3a2,∴b=
ac+a2+c2-ac,化简得c=2a,又b2=a2+c2-ac=3a2,∴b=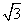 a,
a,
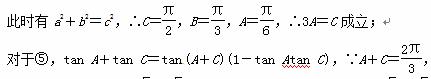 ∴tan A+tan C=-
∴tan A+tan C=-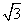 +
+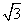 tan Atan C,∵tan A+tan C+
tan Atan C,∵tan A+tan C+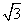 =
=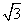 tan Atan C>0,
tan Atan C>0,
又在△ABC中,A、C不能同为钝角,∴A、C都是锐角,∴△ABC为锐角三角形.

练习册系列答案
相关题目
 .若存在
.若存在 ,使得
,使得 成立,则实数
成立,则实数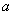 的取值范围是 .
的取值范围是 . 的值为________.
的值为________. <α<π,3sin 2α=2cos α,则cos(α-π)=________.
<α<π,3sin 2α=2cos α,则cos(α-π)=________. .
. ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α< ,求β.
,求β. ,
, .若向量
.若向量 满足
满足 ,
, ,则
,则 .
. 是公差不为0的等差数列,
是公差不为0的等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,
, ,
, ,且存在常数
,且存在常数 ,
, ,使得
,使得 对每一个正整数
对每一个正整数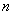 恒成立,则
恒成立,则 =________.
=________.