题目内容
设矩阵M=
.
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(Ⅱ)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C′:x2-2y2=1,求a+b的值.
|
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(Ⅱ)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C′:x2-2y2=1,求a+b的值.
考点:逆变换与逆矩阵
专题:选作题,矩阵和变换
分析:(I)求出M的行列式,即可求矩阵M的逆矩阵M-1;
(Ⅱ)确定坐标之间的变换关系,利用若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C′:x2-2y2=1,比较系数,求出a,b,即可求a+b的值.
(Ⅱ)确定坐标之间的变换关系,利用若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C′:x2-2y2=1,比较系数,求出a,b,即可求a+b的值.
解答:
解:(I)当a=2,b=3时,M的行列式det(M)=-5,
故所求的逆矩阵M-1=
.…(3分)
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),则
=
,即
又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,…(5分)
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得
,解得b=0,a=2,∴a+b=2.…(7分)
故所求的逆矩阵M-1=
|
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),则
|
|
|
|
又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,…(5分)
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得
|
点评:本小题主要考查矩阵与变换等基础知识,考查运算求解能力,考查化归与转化思想.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图所示的四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,点P在底面的射影O在DA的延长线上,且OC过边AB的中点E.
如图所示的四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,点P在底面的射影O在DA的延长线上,且OC过边AB的中点E.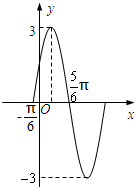 如图f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<