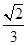题目内容
已知椭圆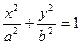 (
(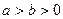 )的两个焦点分别为
)的两个焦点分别为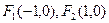 ,点P在椭圆上,且满足
,点P在椭圆上,且满足 ,
,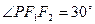 ,直线
,直线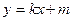 与圆
与圆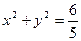 相切,与椭圆相交于A,B两点.
相切,与椭圆相交于A,B两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明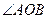 为定值(O为坐标原点)
为定值(O为坐标原点)
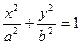 (
(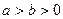 )的两个焦点分别为
)的两个焦点分别为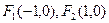 ,点P在椭圆上,且满足
,点P在椭圆上,且满足 ,
,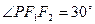 ,直线
,直线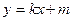 与圆
与圆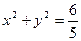 相切,与椭圆相交于A,B两点.
相切,与椭圆相交于A,B两点.(Ⅰ)求椭圆的方程;
(Ⅱ)证明
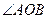 为定值(O为坐标原点)
为定值(O为坐标原点)(Ⅰ)
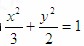
(Ⅱ)证明略
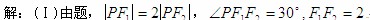

(Ⅱ)设交点
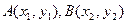 ,联立
,联立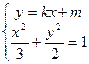 ,
,消去
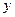 可得
可得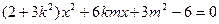
由韦达定理得
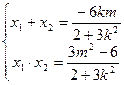 -------------------------9分
-------------------------9分又直线
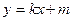 与圆
与圆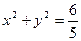 相切,与椭圆相交于A,B两点,
相切,与椭圆相交于A,B两点,从而有
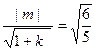 ,即
,即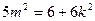 -------------------------11分
-------------------------11分从而
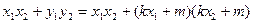

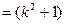
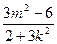 +
+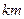
 +
+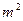
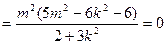
∴
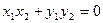 , --------------------------------14分
, --------------------------------14分所以
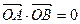 ,即
,即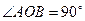 ,即
,即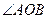 为定值
为定值 。------------15分
。------------15分
练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
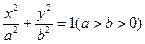 的左右焦点分别为
的左右焦点分别为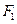 、
、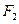 ,离心率
,离心率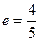 ,直线
,直线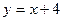 经过椭圆的左焦点
经过椭圆的左焦点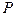 满足:
满足: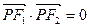 ,求
,求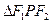 的面积.
的面积. 分)已知椭圆
分)已知椭圆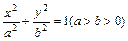 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且 .
.
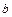 的值;
的值;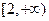 ,使得四边形OACB是平行四边形,请证明你
,使得四边形OACB是平行四边形,请证明你 的结论;
的结论;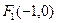 和
和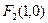 ,离心率
,离心率 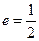
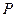 在这个椭圆上,且
在这个椭圆上,且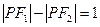 ,求
,求 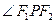 的余弦值.
的余弦值.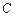 :+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线
:+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线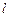 于点M,N为
于点M,N为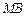 的中点.
的中点.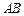 为直径的圆
为直径的圆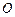 上;
上;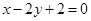 经过椭圆
经过椭圆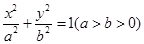 的一个焦点和一个顶点,则该椭圆的离心率为.
的一个焦点和一个顶点,则该椭圆的离心率为.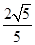
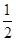
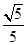
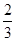
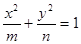 表示焦点在x轴上的椭圆有
表示焦点在x轴上的椭圆有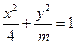 的离心率为
的离心率为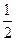 ,则
,则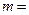 。
。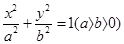 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且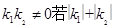 的最小值为1,则椭圆的离心率( )
的最小值为1,则椭圆的离心率( )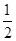 B.
B.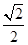 C.
C.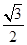 D.
D.