题目内容
设数列{an}的首项a1=4,前n项和为Sn,且满足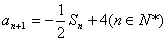 。
。
(1)求{an}的通项公式;
(2)记bn=(1-(-1)n)an+(2n -1)p(n∈N*,p为常数),且b2,b3,b5成等差数列,求b1+b2+ b3+…+b2n。
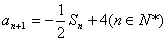 。
。(1)求{an}的通项公式;
(2)记bn=(1-(-1)n)an+(2n -1)p(n∈N*,p为常数),且b2,b3,b5成等差数列,求b1+b2+ b3+…+b2n。
解:(1)由条件,得a1=4,a2=2
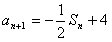
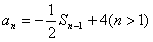
作差,得
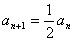
又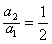
即 。
。
(2)b1=8+p,b2=3p,b3=2+5p,b4=7p
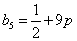 ,
,
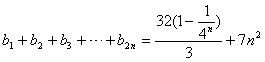 。
。
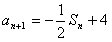
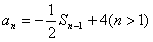
作差,得
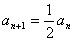
又
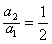
即
 。
。(2)b1=8+p,b2=3p,b3=2+5p,b4=7p
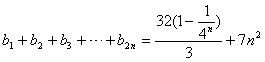 。
。
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
