题目内容
5．方程ax2-3x-1=0至少有一个负数根，则实数a的取值范围是（ ）| A． | （-∞，-$\frac{9}{4}$） | B． | （-∞，-$\frac{9}{4}$] | C． | [-$\frac{9}{4}$，+∞） | D． | [0，+∞） |
分析 分别考虑二次项系数a=0，a≠0，利用二次方程的根与系数关系分别检验方程根的存在情况，可求a的范围．
解答 解：若a=0，则x=-$\frac{1}{3}$，成立；
若a＞0，△=9+4a＞0，由韦达定理知x1•x2=-$\frac{1}{a}$＜0，故此一元二次方程有一个正根和一个负根，故成立；
若a＜0；则只需使△=9+4a≥0即可，
故-$\frac{9}{4}$≤a＜0
综上所述，实数a的取值范围为[-$\frac{9}{4}$，+∞）
故选：C
点评 本题主要考查了方程的根的存在情况的讨论，解题中不要漏掉a=0的考虑，另外还要注意：至少有一负根对方程根的个数的要求．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
16．某几何体的三视图如图所示，则该几何体的体积可以是（ ）
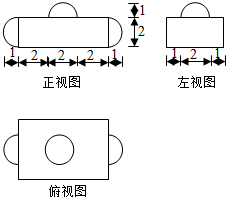
| A． | $48+\frac{4}{3}π$ | B． | 48+2π | C． | $48+\frac{8}{3}π$ | D． | 48+3π |
20．《九章算术》之后，人们进一步地用等差数列求和公式来解决更多的问题．《张邱建算经》卷上第22题为：今有女善织，日益功疾（注：从第2天起每天比前一天多织相同量的布），第一天织5尺布，现在一月（按30天计），共织390尺布，则第2天织的布的尺数为（ ）
| A． | $\frac{161}{29}$ | B． | $\frac{161}{31}$ | C． | $\frac{81}{15}$ | D． | $\frac{80}{15}$ |
17．
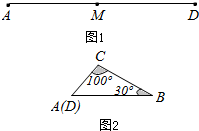如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）
如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）| A． | 点M在AB上 | |
| B． | 点M在BC的中点处 | |
| C． | 点M在BC上，且距点B较近，距点C较远 | |
| D． | 点M在BC上，且距点C较近，距点B较远 |
15．在△ABC中，角A，B，C所对的边分别是a，b，c，已知 sin（B+C）+sin（B-C）=2sin2C，且a=4，A=$\frac{π}{3}$，则△ABC的面积是（ ）
| A． | $\frac{8\sqrt{3}}{3}$ | B． | $\frac{8\sqrt{3}}{4}$ | C． | $\frac{8}{3}$ | D． | $\frac{8\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{4}$ |