题目内容
15.在△ABC中,角A,B,C所对的边分别是a,b,c,已知 sin(B+C)+sin(B-C)=2sin2C,且a=4,A=$\frac{π}{3}$,则△ABC的面积是( )| A. | $\frac{8\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{4}$ | C. | $\frac{8}{3}$ | D. | $\frac{8\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{4}$ |
分析 根据两角和差的正弦公式化简已知式子,利用正弦、余弦定理列出方程,化简求出b的值,代入三角形的面积公式求出△ABC的面积.
解答 解:由题意知,sin(B+C)+sin(B-C)=2sin2C,
则sinBcosC+cosBsinC+sinBcosC-cosBsinC=4sin2C,
2sinBcosC=4sinCcosC,
由0<C<π得cosC≠0,则sinB=2sinC,
由正弦定理得b=2c,又a=4,A=$\frac{π}{3}$,
所以由余弦定理得:a2=b2+c2-2bccosA,
解得c2=$\frac{16}{3}$,则c=$\frac{4\sqrt{3}}{3}$,即b=$\frac{8\sqrt{3}}{3}$,
所以△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×\frac{8\sqrt{3}}{3}×\frac{4\sqrt{3}}{3}×\frac{\sqrt{3}}{2}$=$\frac{8\sqrt{3}}{3}$,
故选:A.
点评 本题考查正弦、余弦定理,两角和差的正弦公式,以及三角形的面积公式,属于中档题.

练习册系列答案
相关题目
5.方程ax2-3x-1=0至少有一个负数根,则实数a的取值范围是( )
| A. | (-∞,-$\frac{9}{4}$) | B. | (-∞,-$\frac{9}{4}$] | C. | [-$\frac{9}{4}$,+∞) | D. | [0,+∞) |
3.函数$f(x)=1o{g_{\frac{1}{2}}}(2{x^2}-ax+3)$在区间[-1,+∞)上是减函数,则实数a的取值范围是( )
| A. | (-∞,-5)∪[-4,+∞) | B. | (-5,-4] | C. | (-∞,-4] | D. | [-4,0) |
10.已知$\overrightarrow{a}$=(5,6),$\overrightarrow{b}$=(sinα,cosα),已知向量且$\overrightarrow{a}$∥$\overrightarrow{b}$,则tanα=( )
| A. | $\frac{5}{6}$ | B. | -$\frac{5}{6}$ | C. | $\frac{6}{5}$ | D. | -$\frac{6}{5}$ |
7.函数f(x)是定义在R上的奇函数,且它是减函数,若实数a,b满足f(a)+f(b)>0,则a与b的关系是( )
| A. | a+b>0 | B. | a+b<0 | C. | a+b=0 | D. | 不确定 |
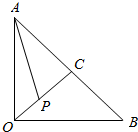 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.