题目内容

17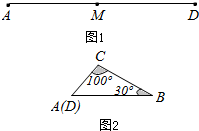．如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（　　）
A．点M在AB上
B．点M在BC的中点处
C．点M在BC上，且距点B较近，距点C较远
D．点M在BC上，且距点C较近，距点B较远

分析 根据钝角三角形中钝角所对的边最长可得AB＞AC，取BC的中点E，求出AB+BE＞AC+CE，再根据三角形的任意两边之和大于第三边得到AB＜$\frac{1}{2}$AD，从而判定AD的中点M在BE上．

解答 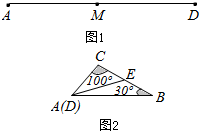解：∵∠C=100°，
∴AB＞AC，
如图，取BC的中点E，则BE=CE，
∴AB+BE＞AC+CE，
由三角形三边关系，AC+BC＞AB，
∴AB＜$\frac{1}{2}$AD，
∴AD的中点M在BE上，
即点M在BC上，且距点B较近，距点C较远．
故选：C．

点评 本题考查了三角形的三边关系，作辅助线把△ABC的周长分成两个部分是解题的关键，本题需要注意判断AB的长度小于AD的一半，这也是容易忽视而导致求解不完整的地方．

练习册系列答案
相关题目
7．某几何体的三视图，如图所示，则该几何体的体积为（　　）
A．72一$\frac{9π}{2}$B．72-4πC．72一$\frac{7π}{2}$D．72-3π
8．函数y=$\sqrt{m{x}^{2}-6mx+m+8}$的定义域是R，则实数m的取值范围是（　　）
A．0＜m≤1B．0≤m≤1C．0＜m＜1D．0≤m＜1
5．方程ax2-3x-1=0至少有一个负数根，则实数a的取值范围是（　　）
A．（-∞，-$\frac{9}{4}$）B．（-∞，-$\frac{9}{4}$]C．[-$\frac{9}{4}$，+∞）D．[0，+∞）
12．函数f（x）=$\left\{\begin{array}{l}-2x，x≤0\\{x^2}+1，x＞0\end{array}$，若f[f（a）]=0，则a=0．
2．设M，P是两个非空集合，定义M与P的差集为：M-P={x|x∈M，且x∉P}，若M={1，2，3，4}，P={3，4，5}则M-P={1，2}，M-（M-P）={3，4}．
9．双曲线C；$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0））的左右焦点分别为F1，F2，双曲线C上一点P到右焦点F2的距离是实轴两端点到右焦点距离的等差中项，若△PF1F2为锐角三角形，则双曲线C的离心率的取值范围是（　　）
A．（$\frac{1+\sqrt{5}}{2}$，+∞）B．（1，1+$\sqrt{3}$）C．（$\frac{1+\sqrt{5}}{2}$，1+$\sqrt{3}$）D．（$\frac{1+\sqrt{5}}{2}$，2）∪（2，1+$\sqrt{3}$）
6．（1）化简 a${\;}^{\frac{2}{3}}$•b${\;}^{\frac{1}{2}}$•（2a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$）÷（$\frac{1}{6}$a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$）； 
（2）计算 （$\sqrt{2}$-1）0+（$\frac{16}{9}$）${\;}^{\frac{1}{2}}$+8${\;}^{\frac{2}{3}}$．
7．函数f（x）是定义在R上的奇函数，且它是减函数，若实数a，b满足f（a）+f（b）＞0，则a与b的关系是（　　）
A．a+b＞0B．a+b＜0C．a+b=0D．不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网