题目内容
若直线l的一般方程为xcosθ+
y-1=0(θ∈R),则直线l的倾斜角的取值范围是 .
| 3 |
考点:直线的倾斜角
专题:直线与圆
分析:由直线方程的一般式求得直线的斜率,进一步得到斜率得范围,再由倾斜角的正切值等于斜率求得直线倾斜角的范围.
解答:
解:由直线l的一般方程为xcosθ+
y-1=0(θ∈R)得其斜率为k=-
cosθ,
∴k∈[-
,
].
设直线l的倾斜角为α,
则由tanα∈[-
,
],
得α∈[0,
]∪[
,π].
故答案为:[0,
]∪[
,π].
| 3 |
| ||
| 3 |
∴k∈[-
| ||
| 3 |
| ||
| 3 |
设直线l的倾斜角为α,
则由tanα∈[-
| ||
| 3 |
| ||
| 3 |
得α∈[0,
| π |
| 6 |
| 5π |
| 6 |
故答案为:[0,
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查直线的倾斜角与斜率,考查了正切函数的单调性,是中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
在△ABC中,已知2acosB=c,|
+
|=|
-
|,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、等边三角形 |
| B、等腰直角三角形 |
| C、锐角非等边三角形 |
| D、钝角三角形 |
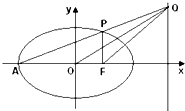 如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C:
如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C: