题目内容
已知|
|=1，若非零向量
满足
•（
-
）=0，则|
|的取值范围为
| a |
| b |
| b |
| b |
| a |
| b |
（0，1]
（0，1]
．分析：根据题意分两类：
=
≠
和
≠
，当
≠
时，根据
•(
-
)=0画出图形，判断出
，
夹角范围，再把
•(
-
)=0展开化简，由向量夹角余弦值的范围求出|
|的范围．
| b |
| a |
| 0 |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
解答：解：①当
=
≠
时，满足
•(
-
)=0，此时|
|=1，
②由
≠
时，
•(
-
)=0得，
⊥(
-
)，根据向量减法的几何意义画出示意图，
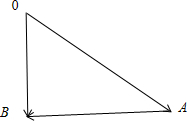
如图：在RT△OAB中，设
=
，
=
，则
=
-
，
∴
，
之间的夹角为∠AOB，则∠AOB∈（0，
），
由
•(
-
)=0得，
2-
•
=0，即|
| -cos∠AOB=0，
∴|
| =cos∠AOB∈（0，1），
综上得，|
| ∈(0，1]．
故答案为：（0，1]．
| b |
| a |
| 0 |
| b |
| b |
| a |
| b |
②由
| b |
| a |
| b |
| b |
| a |
| b |
| b |
| a |
如图：在RT△OAB中，设
| b |
| 0B |
| a |
| OA |
| AB |
| b |
| a |
∴
| b |
| a |
| π |
| 2 |
由
| b |
| b |
| a |
| b |
| b |
| a |
| b |
∴|
| b |
综上得，|
| b |
故答案为：（0，1]．
点评：本题考查了向量数量积的运算，向量减法的几何意义，以及垂直的等价条件，易忘
=
≠
的情况．
| b |
| a |
| 0 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目