题目内容
设等差数列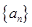 的前
的前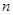 项和
项和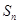 ,且
,且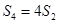 ,
,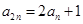 .
.
(1)求数列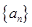 的通项公式;
的通项公式;
(2)若数列满足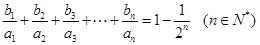 ,求数列
,求数列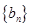 的前
的前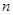 项和
项和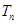 .
.
(1) .(2)
.(2) ,
, .
.
解析试题分析:(1)确定等差数列的通项公式,往往利用已知条件,建立相关元素的方程组,如本题,设等差数列 的公差为
的公差为 ,结合已知,可建立
,结合已知,可建立 的方程组,
的方程组, ,解得
,解得 得到
得到 .
.
(2)首先应确定 。然后利用“错位相减法”求得
。然后利用“错位相减法”求得 .
.
试题解析:(1)设等差数列 的公差为
的公差为 ,
,
由 得
得 2分
2分 解得
解得 4分
4分
故通项公式为 5分
5分
(2)由已知 ①
① 时,
时, 6分
6分 时,
时, ②
②
① ②得:
②得: 对于
对于 也成立
也成立
故 8分
8分
所以 9分
9分 ③
③ ④ 10分
④ 10分
③ ④得:
④得: 11分
11分 12分
12分

所以 14分
14分
考点:等差数列、等比数列的通项公式,“错位相减法”求和.

练习册系列答案
相关题目
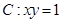 ,过
,过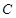 上一点
上一点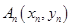 作一斜率为
作一斜率为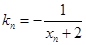 的直线交曲线
的直线交曲线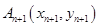 (
(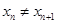 且
且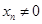 ,点列
,点列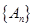 的横坐标构成数列
的横坐标构成数列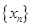 ,其中
,其中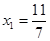 .
.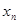 与
与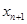 的关系式;
的关系式;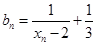 ,求证:数列
,求证:数列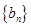 是等比数列;
是等比数列;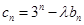 (
( 为非零整数,
为非零整数,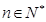 ),试确定
),试确定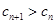 成立.
成立. 是等差数列,且
是等差数列,且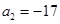 ,
,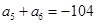 ;又若
;又若 是各项为正数的等比数列,且满足
是各项为正数的等比数列,且满足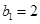 ,其前
,其前 项和为
项和为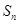 ,
,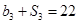 .
.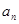 ,
,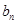 ;
;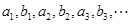 的前
的前 ,求
,求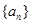 的各项均为正数,
的各项均为正数,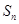 为其前
为其前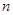 项和,对于任意的
项和,对于任意的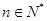 ,满足关系式
,满足关系式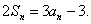
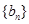 的通项公式是
的通项公式是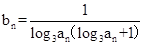 ,前
,前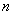 项和为
项和为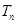 ,求证:对于任意的正整数
,求证:对于任意的正整数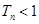 .
.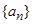 中,
中,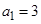 ,前
,前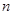 和
和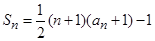
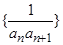 的前
的前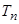 ,是否存在实数
,是否存在实数 ,使得
,使得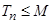 对一切正整数
对一切正整数 的前
的前 项和
项和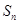 ,满足:
,满足: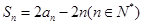 .
.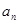 ;
;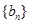 的满足
的满足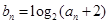 ,
,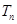 为数列
为数列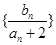 的前
的前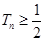 .
.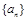 和公比为
和公比为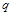
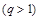 的等比数列
的等比数列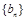 满足:
满足: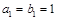 ,
,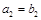 ,
, .
.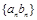 的前
的前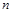 项和为
项和为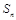 ,且对任意
,且对任意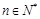 均有
均有 成立,试求实数
成立,试求实数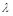 的取值范围.
的取值范围.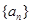 :
: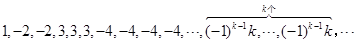 ,即当
,即当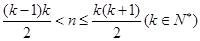 时,记
时,记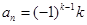 .记
.记 . 对于
. 对于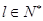 ,定义集合
,定义集合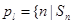 是
是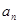 的整数倍,
的整数倍,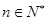 ,且
,且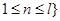 .
.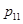 中元素的个数;
中元素的个数;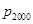 中元素的个数.
中元素的个数. ,规定
,规定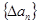 为数列
为数列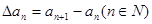 , 对自然数
, 对自然数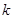 ,规定
,规定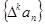 为
为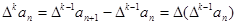 .
.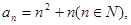 ,试判断
,试判断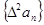 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?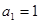 ,且满足
,且满足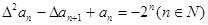 ,求数列
,求数列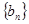 ,使得
,使得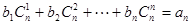 对一切自然
对一切自然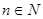 都成立?若存在,求数列
都成立?若存在,求数列