题目内容
已知数列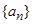 中,
中,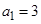 ,前
,前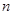 和
和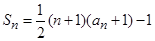
(Ⅰ)求证:数列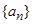 是等差数列; (Ⅱ)求数列
是等差数列; (Ⅱ)求数列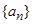 的通项公式;
的通项公式;
(Ⅲ)设数列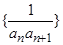 的前
的前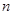 项和为
项和为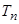 ,是否存在实数
,是否存在实数 ,使得
,使得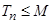 对一切正整数
对一切正整数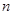 都成立?若存在,求
都成立?若存在,求 的最小值,若不存在,试说明理由.
的最小值,若不存在,试说明理由.
(Ⅰ)详见解析;(Ⅱ)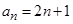 ;(Ⅲ)存在,
;(Ⅲ)存在,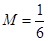 .
.
解析试题分析:(Ⅰ)对条件式进行变形,得到递推关系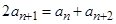 得证;(Ⅱ)由条件求出首项和公差即得;(Ⅲ)利用裂项相消法求出
得证;(Ⅱ)由条件求出首项和公差即得;(Ⅲ)利用裂项相消法求出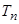 ,再考察
,再考察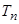 的上确界,可得
的上确界,可得 的最小值.
的最小值.
试题解析:(Ⅰ)因为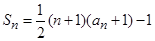 ,所以
,所以 ,
,
所以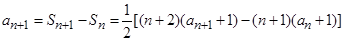 ,
,
整理,得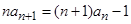 ,所以
,所以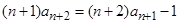 ,
,
所以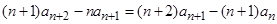 ,
,
所以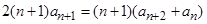 ,所以
,所以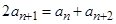 ,
,
所以,数列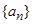 为等差数列。
为等差数列。
(Ⅱ)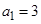 ,
,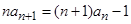 ,所以
,所以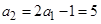 ,
,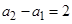 即为公差,
即为公差,
所以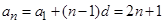 ;
;
(Ⅲ)因为 ,
,
所以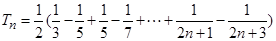
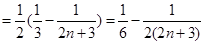 ,
,
所以对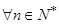 时,
时,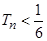 ,且当
,且当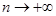 时,
时,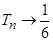 ,所以要使
,所以要使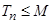 对一切正整数
对一切正整数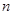 都成立,只要
都成立,只要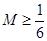 ,所以存在实数
,所以存在实数 使得
使得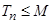 对一切正整数
对一切正整数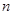 都成立,
都成立, 的最小值为
的最小值为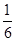 .
.
考点:等差数列、数列的求和、不等式、裂项相消法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,
,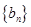 满足
满足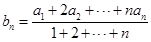
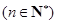 .
.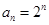 ,求数列
,求数列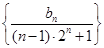 的前
的前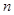 项和
项和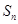 .
.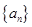 满足递推式:
满足递推式: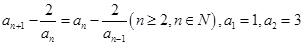 .
.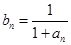 ,求
,求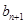 与
与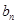 的递推关系(用
的递推关系(用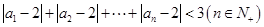 .
. 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在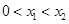 ,使得不等式
,使得不等式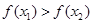 成立 设数列
成立 设数列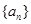 的前
的前 项和为
项和为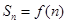
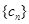 中,所有满足
中,所有满足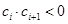 的正整数
的正整数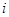 的个数称为这个数列
的个数称为这个数列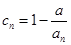 (
( 的前
的前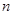 项和为
项和为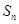 ,对任意正整数
,对任意正整数 ,记
,记 .
.  ,
, 的值;
的值; 的通项公式;
的通项公式;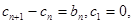 求证:对任意
求证:对任意 .
.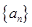 的前
的前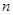 项和
项和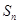 ,且
,且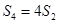 ,
,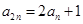 .
.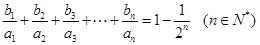 ,求数列
,求数列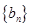 的前
的前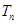 .
.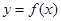 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为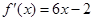 ,数列
,数列 的前
的前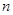 项和为
项和为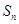 ,点
,点 均在函数
均在函数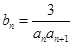 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有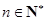 都成立的最小正整数
都成立的最小正整数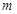 .
.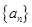 满足
满足 ,且
,且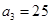 .
. 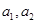
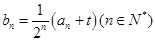 ,且{
,且{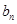 }为等差数列?若存在,求出t的值;若不存在,说明理由.
}为等差数列?若存在,求出t的值;若不存在,说明理由. 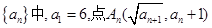 在抛物线
在抛物线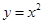 上;数列
上;数列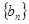 中,点
中,点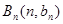 在过点(0,1),以
在过点(0,1),以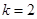 为斜率的直线上。
为斜率的直线上。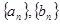 的通项公式;
的通项公式; 成立,若存在,求出k值;若不存在,请说明理由;
成立,若存在,求出k值;若不存在,请说明理由;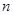 ,不等式
,不等式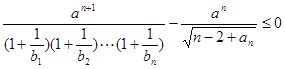 恒成立,求正数
恒成立,求正数 的取值范围。
的取值范围。