题目内容
求函数f(x)=
的最大值和最小值.
| x2-2x-3 |
| 2x2+2x+1 |
考点:基本不等式
专题:函数的性质及应用
分析:将函数y=f(x)=
变形为(2y-1)x2+(2y+2)x+y+3=0,由于分母2x2+2x+1=2(x+
)2+
>0,可得函数f(x)的定义域为R.对y分类讨论:当y=
时,原式变为6x=-7,可得得x=-
.当y≠
时,上式对于任意实数x都成立,可得△=(2y+2)2-4(2y-1)(y+3)≥0,解出即可.
| x2-2x-3 |
| 2x2+2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 6 |
| 1 |
| 2 |
解答:
解:将函数y=f(x)=
变形为(2y-1)x2+(2y+2)x+y+3=0,
∵分母2x2+2x+1=2(x+
)2+
>0,∴函数f(x)的定义域为R.
①当y=
时,原式变为6x=-7,解得x=-
.因此y=
也满足题意.
②当y≠
时,上式对于任意实数x都成立,因此△=(2y+2)2-4(2y-1)(y+3)≥0,
化为y2+3y-4≤0,
解得-4≤y≤1,且y≠
.
综上可知:-4≤y≤1.
当x=-2时,函数f(x)取得最大值1;
当x=-
时,函数f(x)取得最小值-4.
| x2-2x-3 |
| 2x2+2x+1 |
∵分母2x2+2x+1=2(x+
| 1 |
| 2 |
| 1 |
| 2 |
①当y=
| 1 |
| 2 |
| 7 |
| 6 |
| 1 |
| 2 |
②当y≠
| 1 |
| 2 |
化为y2+3y-4≤0,
解得-4≤y≤1,且y≠
| 1 |
| 2 |
综上可知:-4≤y≤1.
当x=-2时,函数f(x)取得最大值1;
当x=-
| 1 |
| 3 |
点评:本题考查了利用“判别式法”求分式类型函数的最值,考查了推理能力和计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
相关题目
 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[90,100)、[90,100].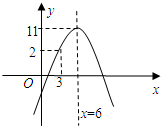 某汽车运输公司,购买了一批豪华大客车投入客运,据市场分析,每辆客车营运的总利润y(万元)与营运年数x(x∈N*)的二次函数关系如图,为了使每辆客车营运的年平均利润最大,则每辆客车应营运
某汽车运输公司,购买了一批豪华大客车投入客运,据市场分析,每辆客车营运的总利润y(万元)与营运年数x(x∈N*)的二次函数关系如图,为了使每辆客车营运的年平均利润最大,则每辆客车应营运