题目内容
设a=(-1,1),b=(4,3),c=(5,-2),
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求 1和
1和 2,使c=
2,使c= 1a+
1a+ 2b.
2b.
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求
 1和
1和 2,使c=
2,使c= 1a+
1a+ 2b.
2b.(1)证明见解析(2)- (3)
(3) 1=-
1=- ,
, 2=
2= .
.
 (3)
(3) 1=-
1=- ,
, 2=
2= .
.(1)证明 ∵a=(-1,1),b=(4,3),-1×3≠1×4,
∴a与b不共线,设a与b的夹角为 ,
,
cos =
= =
= =-
=- .
.
(2)解 设a与c的夹角为 ,
,
cos =
= =
= =-
=- ,
,
∴c在a方向上的投影为
|c|cos =-
=- .
.
(3)解 ∵c= 1a+
1a+ 2b,∴
2b,∴ ,
,
解得 1=-
1=- ,
, 2=
2= .
.
∴a与b不共线,设a与b的夹角为
 ,
,cos
 =
= =
= =-
=- .
.(2)解 设a与c的夹角为
 ,
,cos
 =
= =
= =-
=- ,
,∴c在a方向上的投影为
|c|cos
 =-
=- .
.(3)解 ∵c=
 1a+
1a+ 2b,∴
2b,∴ ,
,解得
 1=-
1=- ,
, 2=
2= .
.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 ,
, ,
, 与
与 不共线,
不共线,  与
与 垂直;
垂直; 与
与 的模相等,试求角
的模相等,试求角 .
.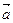 =(
=(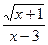 ,1),
,1),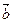 =(x,x2),
=(x,x2),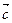 =(-3,-x2+x),函数f(x)=
=(-3,-x2+x),函数f(x)=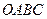 中,已知过点
中,已知过点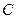 的直线与线段
的直线与线段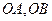 分别相交于点
分别相交于点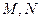 。若
。若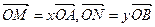 。
。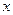 与
与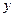 的关系为
的关系为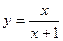 ;
;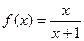 ,定义函数
,定义函数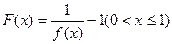 ,点列
,点列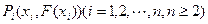 在函数
在函数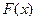 的图像上,且数列
的图像上,且数列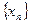 是以首项为1,公比为
是以首项为1,公比为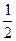 的等比数列,
的等比数列,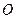 为原点,令
为原点,令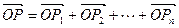 ,是否存在点
,是否存在点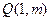
 ,使得
,使得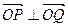 ?若存在,请求出
?若存在,请求出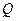 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。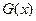 为
为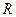 上偶函数,当
上偶函数,当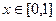 时
时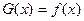 ,又函数
,又函数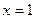 对称,当方程
对称,当方程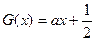 在
在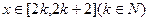 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数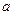 的取值范围。
的取值范围。
 )的值;(2)写出f(x)在
)的值;(2)写出f(x)在 上的单调递增区间
上的单调递增区间 、
、 、
、 满足条件
满足条件 ,
, ,试判断△P1P2P3的形状,并加以证明。
,试判断△P1P2P3的形状,并加以证明。 ,
, ,
, ,
, .
. 时,求使不等式
时,求使不等式 成立的x的取值范围;
成立的x的取值范围; 成立的x的取值范围.
成立的x的取值范围. ,
, ,求
,求 及
及 、
、 间的夹角
间的夹角 (精确到
(精确到 ).
).