题目内容
Sn表示等差数列{an}的前n项的和,且S4=S9,a1=-12(1)求数列的通项an及Sn;
(2)求和Tn=|a1|+|a2|+…+|an|
【答案】分析:(1)由已知结合等差数列前n项和公式,构造关于公差d的方程,求出公差后,可得数列的通项an及Sn;
(2)由(1)中数列的通项公式,可得数列前6项为负,故可分n≤6和n≥7时两种情况,结合等差数列前n项和公式求Tn.
解答:解:(1)∵S4=S9,a1=-12,
∴4×(-12)+6d=9×(-12)+36d
解得d=2…(3分)
∴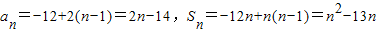 …(7分)
…(7分)
(2)当n≤6时,an<0,|an|=-an,
Tn=-(a1+a2+…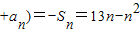 =13n-n2,…(10分)
=13n-n2,…(10分)
当n≥7时,an≥0,
Tn=-(a1+a2+…+a6)+(a7+…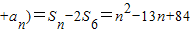
=Sn-2(a1+a2+…+a6)
=n2-13n+84…(14分)
点评:本题考查的知识点是等差数列的通项公式和前n项公式,其中(2)由于Tn的表达式中出现绝对值,故要分析各项符号.
(2)由(1)中数列的通项公式,可得数列前6项为负,故可分n≤6和n≥7时两种情况,结合等差数列前n项和公式求Tn.
解答:解:(1)∵S4=S9,a1=-12,
∴4×(-12)+6d=9×(-12)+36d
解得d=2…(3分)
∴
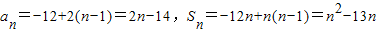 …(7分)
…(7分)(2)当n≤6时,an<0,|an|=-an,
Tn=-(a1+a2+…
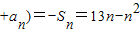 =13n-n2,…(10分)
=13n-n2,…(10分)当n≥7时,an≥0,
Tn=-(a1+a2+…+a6)+(a7+…
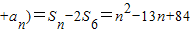
=Sn-2(a1+a2+…+a6)
=n2-13n+84…(14分)
点评:本题考查的知识点是等差数列的通项公式和前n项公式,其中(2)由于Tn的表达式中出现绝对值,故要分析各项符号.

练习册系列答案
相关题目
已知Sn表示等差数列{an}的前n项和,且
=
,那么
=( )
| S5 |
| S10 |
| 1 |
| 3 |
| S5 |
| S20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设Sn表示等差数列{an}的前n项和,已知
=
,那么
等于( )
| S5 |
| S10 |
| 1 |
| 3 |
| S10 |
| S20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 的前n项和,且
的前n项和,且 ( )
( ) B、
B、 C、
C、 D、
D、
 =
= ,那么
,那么 =( )
=( )


