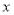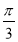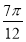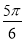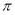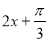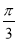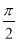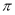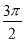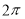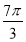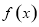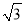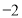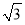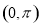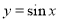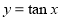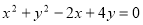题目内容
已知函数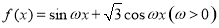 的周期为
的周期为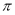 .
.

(1)若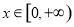 ,求它的振幅、初相;
,求它的振幅、初相;
(2)在给定的平面直角坐标系中作出该函数在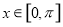 的图像;
的图像;
(3)当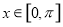 时,根据实数
时,根据实数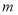 的不同取值,讨论函数
的不同取值,讨论函数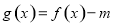 的零点个数.
的零点个数.
(1)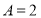 ,
,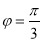 ;(2)详见解析;(3)当
;(2)详见解析;(3)当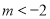 或
或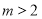 时,函数
时,函数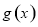 无零点;当
无零点;当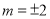 时,函数
时,函数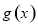 仅有一个零点;当
仅有一个零点;当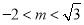 或
或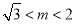 时,函数
时,函数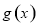 有两个零点;当
有两个零点;当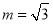 时,函数
时,函数 有三个零点.
有三个零点.
【解析】
试题分析:(1)先由辅助角公式化简,然后由周期为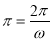 确定
确定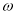 ,可确定
,可确定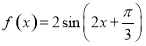 ,从而可写出振幅、初相;(2)根据正弦函数的五点作图法进行作图即可;(3)将
,从而可写出振幅、初相;(2)根据正弦函数的五点作图法进行作图即可;(3)将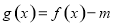 的零点问题,转化为直线
的零点问题,转化为直线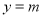 与函数
与函数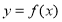 的图像交点的个数问题,结合(2)中作出的函数
的图像交点的个数问题,结合(2)中作出的函数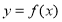 的图像,对直线的位置进行讨论,可得答案.
的图像,对直线的位置进行讨论,可得答案.
试题解析:(1)化为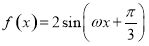 1分
1分
由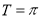 得,
得, 即
即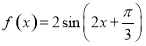 2分
2分
(1)函数的振幅是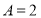 ,初相为
,初相为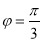 4分
4分
(2)列表
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 |
| 0 |
|
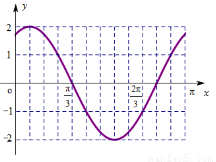 8分
8分
(3)函数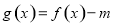 在
在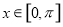 的零点个数,即函数
的零点个数,即函数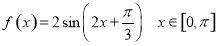 与函数
与函数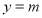 的交点个数,由(2)图像知:
的交点个数,由(2)图像知:
①当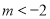 或
或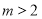 时,函数
时,函数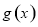 无零点;
无零点;
②当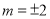 时,函数
时,函数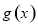 仅有一个零点;
仅有一个零点;
③当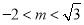 或
或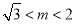 时,函数
时,函数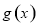 有两个零点;
有两个零点;
④当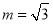 时,函数
时,函数 有三个零点 12分.
有三个零点 12分.
考点:1.辅助角公式;2.三角函数的图像与性质;3.方程的解与函数的零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目