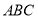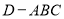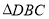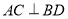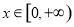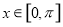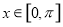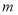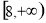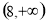题目内容
设
是两条不同的直线，
是三个不同的平面，给出下列四个命题：
①若
，
，则
②若
，
，
，则
③若
，
，
，则
④若
，
，
，则
正确命题的个数是( )
A．1 B．2 C．3 D．4
D
【解析】
试题分析：直线与平面平行与垂直，平面与平面平行与垂直的判定与性质，对选项进行逐一判断，推出结果即可．
①若
，则
，是直线和平面垂直的判定，正确；
②若
，则
，推出
，满足直线和平面垂直的判定，正确；
③若
，则
，根据平面与平面平行的性质“如果两个平面平行并与第三个平面相交，则交线平行”可知命题正确．
④若
，则，根据线面垂直的性质定理可知正确，若一条直线与一个平面的两条相交直线垂直，则该直线与这个平面垂直．
考点：本题考查直线与平面平行与垂直的判定、平面与平面的平行与垂直的判断，考查空间想象能力，逻辑思维能力．
练习册系列答案
备战中考寒假系列答案
相关题目
