题目内容
用白铁皮做一个平底、圆锥形盖的圆柱形粮囤,粮囤容积为 (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为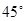 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R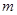 ,需用白铁皮的面积记为
,需用白铁皮的面积记为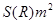 (不计接头等)。
(不计接头等)。
(1)将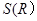 表示为R的函数;
表示为R的函数;
(2)求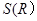 的最小值及对应的粮囤的总高度。(含圆锥顶盖)
的最小值及对应的粮囤的总高度。(含圆锥顶盖)
(1)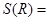
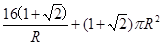 ,(2)
,(2)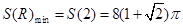 ,对应粮囤的总高度为
,对应粮囤的总高度为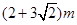 .
.
解析试题分析:(1)立体几何应用题,实际考查立体几何的侧面积. 根据圆锥及圆柱侧面积公式得: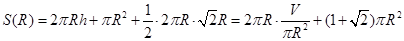
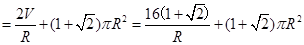 (
(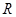 >0),(2)对复杂函数,利用导数求函数最值.由
>0),(2)对复杂函数,利用导数求函数最值.由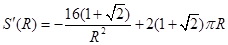 ,令
,令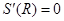 ,得
,得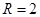 ,当
,当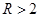 时,
时,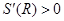 ,当
,当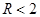 时
时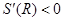 ,所以当
,所以当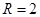 时,
时,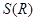 取得极小值也是最小值,且
取得极小值也是最小值,且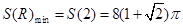 ,此时圆柱的高为
,此时圆柱的高为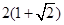 ,圆锥盖的高为
,圆锥盖的高为 ,所以粮囤的总高度为
,所以粮囤的总高度为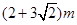 .
.
试题解析:(1)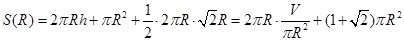
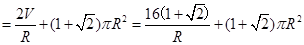 (
(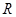 >0) 7分
>0) 7分
(2)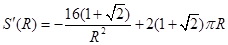 ,令
,令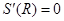 ,得
,得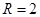 10分
10分
当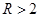 时,
时,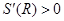 ,当
,当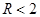 时
时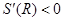 ,所以当
,所以当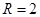 时,
时,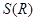 取得极小值也是最小值,且
取得极小值也是最小值,且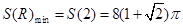 , 13分
, 13分
此时圆柱的高为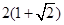 ,圆锥盖的高为
,圆锥盖的高为 ,所以粮囤的总高度为
,所以粮囤的总高度为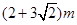 15分
15分
答:(1)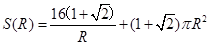 ;(2)
;(2)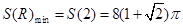 ,对应粮囤的总高度为
,对应粮囤的总高度为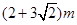 。 16分
。 16分
考点:圆锥及圆柱侧面积,利用导数求最值

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
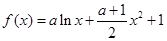 .
.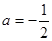 时,求
时,求 在区间
在区间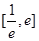 上的最值;
上的最值;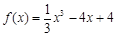 .
.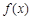 的极值;
的极值;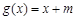 ,对
,对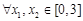 ,都有
,都有 ,求实数m的取值范围.
,求实数m的取值范围.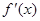 是
是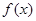 的导函数,
的导函数, ,且函数
,且函数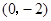 .
.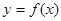 的表达式;
的表达式;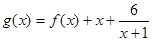 的单调区间和极值.
的单调区间和极值.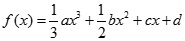 的图像过原点,且在点
的图像过原点,且在点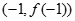 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意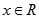 ,都有
,都有 .
. 在点
在点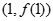 处切线的斜率;
处切线的斜率; 的解析式;
的解析式;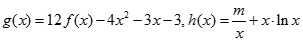 ,对任意
,对任意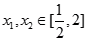 ,都有
,都有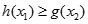 .求实数
.求实数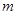 的取值范围.
的取值范围.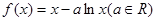
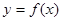 在点
在点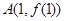 处的切线方程;
处的切线方程; 的极值.
的极值.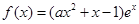 ,其中
,其中 是自然对数的底数,
是自然对数的底数,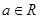 .
.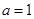 ,求曲线
,求曲线 在点
在点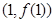 处的切线方程;
处的切线方程;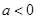 ,求
,求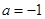 ,函数
,函数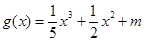 的图像有3个不同的交点,求实数
的图像有3个不同的交点,求实数 的取值范围.
的取值范围.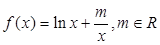 .
.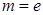 (
(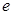 为自然对数的底数)时,求
为自然对数的底数)时,求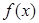 的最小值;
的最小值;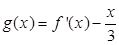 零点的个数;
零点的个数;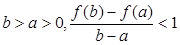 恒成立,求
恒成立,求 的取值范围.
的取值范围.