题目内容
函数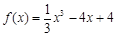 .
.
(1)求函数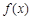 的极值;
的极值;
(2)设函数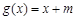 ,对
,对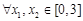 ,都有
,都有 ,求实数m的取值范围.
,求实数m的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:解题思路:(1)求导,令 得
得 ,列表即可极值;(2)因为
,列表即可极值;(2)因为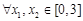 ,都有
,都有 ,所以只需
,所以只需 即可,即求
即可,即求 的最值.规律总结:(1)利用导数求函数的极值的步骤:①求导;②解
的最值.规律总结:(1)利用导数求函数的极值的步骤:①求导;②解 ,得分界点;③列表求极值点及极值;(2)恒成立问题要转化为求函数的最值问题.注意点:因为
,得分界点;③列表求极值点及极值;(2)恒成立问题要转化为求函数的最值问题.注意点:因为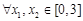 ,都有
,都有 ,所以只需
,所以只需 即可.
即可.
试题解析:(1)因为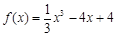 ,所以
,所以 ,
,
令 ,解得
,解得 ,或
,或 ,则
,则x 
-2 
2 
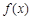
+ 0 - 0 + 
↗ 
↘ 
↗
故当 时,
时,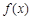 有极大值,极大值为
有极大值,极大值为 ;
;
当 时,
时,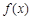 有极小值,极小值为
有极小值,极小值为 .
.
(2)因为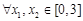 ,都有
,都有 ,所以只需
,所以只需 即可.
即可.
由(1)知:函数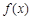 在区间
在区间 上的最小值
上的最小值
 ,
,

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

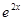 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
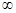 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.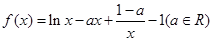
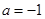 时,求曲线
时,求曲线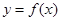 在点
在点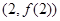 处的切线方程;
处的切线方程;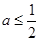 时,讨论
时,讨论 的单调性.
的单调性.
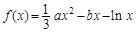 ,其中a,b∈R
,其中a,b∈R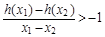 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.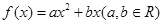 ,函数
,函数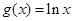 .
.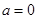 时,函数
时,函数 的图象与函数
的图象与函数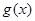 的图象有公共点,求实数
的图象有公共点,求实数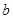 的最大值;
的最大值;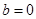 时,试判断函数
时,试判断函数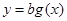 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.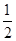 .
. (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为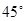 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R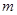 ,需用白铁皮的面积记为
,需用白铁皮的面积记为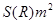 (不计接头等)。
(不计接头等)。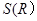 表示为R的函数;
表示为R的函数;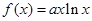
 ,已知曲线
,已知曲线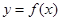 在点
在点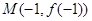 处的切线方程是
处的切线方程是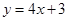 .
.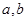 的值;并求出函数的单调区间;
的值;并求出函数的单调区间; 在区间
在区间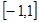 上的最值.
上的最值. 及其导函数
及其导函数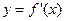 的图象如图所示,则曲线
的图象如图所示,则曲线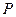 处的切线方程是___▲___.
处的切线方程是___▲___.