题目内容
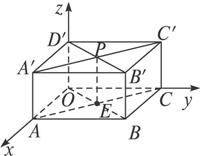
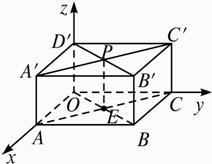
如图,长方体OABC—D'A'B'C'中，|OA|=3,|OC|=5,|OD'|=3,A'C'与B'D'相交于点P，分别写出点C、B'、P的柱坐标.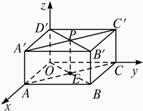
解:求点的柱坐标,需要找到空间任意一点P在Oxy平面上的射影及在平面Oxy上的极坐标(ρ,θ)(ρ≥0,0≤θ＜2π).?
C点的ρ、θ为|OC|及∠COA；
B′点的ρ、θ分别为|OB|=
θ=∠BOA,tan∠BOA=
∴∠BOA=arctan
.P点的ρ、θ为OE、∠AOE,|OE|=
|OB|,∠AOE=∠AOB.?
∴C点的柱坐标为(5,
,0)；B′点的柱坐标为(
,arctan
,3)；P点的柱坐标为(
,arctan
,3).
练习册系列答案
优加精卷系列答案
相关题目
如图，长方体OABC-D'A'B'C'中，|OA|=3，|OC|=4，|OD'|=3，A'C'于B'D'相交于点P．分别写出C，B'，P的坐标．
