题目内容
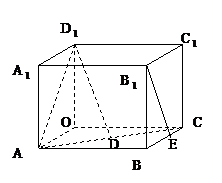
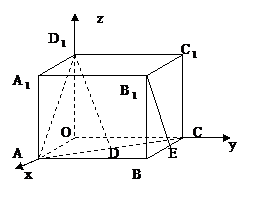
如图所示,在长方体OABC—O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点.
(1)求直线AO1与B1E所成角的大小;
(2)作O1D⊥AC于D,求点O1到点D的距离.
解析:(1)以O为原点,分别以![]() 、
、![]() 、
、![]() 为Ox轴,Oz轴的正向,如图建立空间直角坐标系.
为Ox轴,Oz轴的正向,如图建立空间直角坐标系.

∵|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,
∴A(2,0,0),O1(0,0,2),B1(2,3,2),E(1,3,0),
∴![]() =(-2,0,2),
=(-2,0,2), ![]() =(-1,0,-2),设
=(-1,0,-2),设![]() 与
与![]() 的夹角为θ,则cosθ
的夹角为θ,则cosθ
= =-
=-![]() .
.
∴θ=π-arccos![]() ,则直线AO1与B1E所成角为arccos
,则直线AO1与B1E所成角为arccos![]() .
.
(2)连结OD.
∵O1D⊥AC,∴OD⊥AC,设D坐标为(x,y,0),
由
得
![]()

![]()
 或
或![]() (舍去).
(舍去).
∴点D的坐标为(![]() ,
,![]() ,0).
,0).
∴![]() =(
=(![]() ,
,![]() ,-2).
,-2).
∴|![]() |=
|=![]() =
=![]() .
.
∴点O1到点D的距离为![]() .
.

练习册系列答案
相关题目
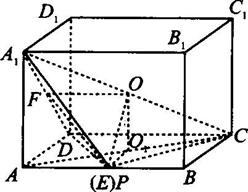
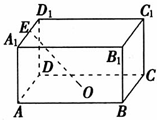 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=2AA1=4,点O是底面ABCD的中心,点E是A1D1的中点,点P是底面ABCD上的动点,且到直线OE的距离等于1.设点P的轨迹为L,则L的离心率等于