题目内容
5.已知向量$\overrightarrow a=({1,cos2x}),\overrightarrow b=({sin2x,-\sqrt{3}})$,函数$f(x)=\overrightarrow a•\overrightarrow b$.(Ⅰ)若$f({\frac{θ}{2}+\frac{2π}{3}})=\frac{6}{5}$,求cos2θ的值;
(Ⅱ)若$x∈[{0,\frac{π}{2}}]$,求函数f(x)的值域.
分析 (I)化简f(x),根据$f({\frac{θ}{2}+\frac{2π}{3}})=\frac{6}{5}$求出sinθ,代入二倍角公式;
(II)根据x的范围求出2x-$\frac{π}{3}$的范围,结合正弦函数的图象与性质得出.
解答 解:(Ⅰ)$f(x)=\vec a•\vec b=sin2x-\sqrt{3}cos2x=2sin(2x-\frac{π}{3})$,
∴f($\frac{θ}{2}+\frac{2π}{3}$)=2sin(θ+π)=-2sinθ=$\frac{6}{5}$,∴sinθ=-$\frac{3}{5}$.
∴cos2θ=1-2sin2θ=1-$\frac{18}{25}$=$\frac{7}{25}$.
(Ⅱ)由$x∈[0,\frac{π}{2}]$,则$2x-\frac{π}{3}∈[-\frac{π}{3},\frac{2π}{3}]$,
∴当2x-$\frac{π}{3}$=-$\frac{π}{3}$时,f(x)取得最小值-$\sqrt{3}$,当2x-$\frac{π}{3}$=$\frac{π}{2}$时,f(x)取得最大值2.
∴f(x)的值域为$[-\sqrt{3},2]$.
点评 本题考查了三角函数的恒等变换和求值,利用三角函数公式对f(x)化简是关键.

练习册系列答案
相关题目
20.已知点P是函数y=sin(x+θ)图象与x轴的一个交点,A,B为P点右侧同一周期上的最大和最小值点,则$\overrightarrow{PA}•\overrightarrow{PB}$=( )
| A. | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B. | $\frac{{3{π^2}}}{4}-1$ | C. | $\frac{{3{π^2}}}{2}-1$ | D. | $\frac{π^2}{2}-1$ |
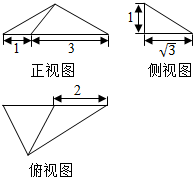
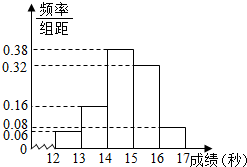 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.