题目内容
已知向量
=(x2-1,2+x),
=(x,1),若
∥
,则x= .
| a |
| b |
| a |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:直接由向量共线的坐标表示列式求解x的值.
解答:
解:∵
=(x2-1,2+x),
=(x,1),
由
∥
,
得(x2-1)-x•(2+x)=0,
解得:x=-
.
故答案为:-
.
| a |
| b |
由
| a |
| b |
得(x2-1)-x•(2+x)=0,
解得:x=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0.是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
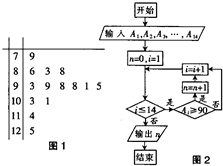 如图1是某高三学生14次数学考试成绩的茎叶图,现将该14个数据依次记为A1,A2,…A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出的n值是( )
如图1是某高三学生14次数学考试成绩的茎叶图,现将该14个数据依次记为A1,A2,…A14,并输入如图2所示的一个算法流程图,那么该算法流程图运行结束时输出的n值是( )