题目内容
在R上定义运算⊕:x⊕y=(1-x)y,若不等式(x+a)⊕(x-a)<1对任意实数x都成立,则a的取值范围是
(0,1)
(0,1)
.分析:由运算⊕可得:不等式(x+a)⊕(x-a)<1对任意实数x都成立?[1-(x+a)](x-a)<1对任意实数x成立,化为a2-a<x2,利用x2≥0解出即可.
解答:解:由运算⊕可得:不等式(x+a)⊕(x-a)<1对任意实数x都成立?[1-(x+a)](x-a)<1对任意实数x成立,
化为a2-a<x2,
∵x2≥0,∴a2-a<0,
解得0<a<1.
∴a的取值范围是(0,1).
故答案为(0,1).
化为a2-a<x2,
∵x2≥0,∴a2-a<0,
解得0<a<1.
∴a的取值范围是(0,1).
故答案为(0,1).
点评:本题考查了新定义、恒成立问题的等价转化、一元二次不等式的解法等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
 :x
:x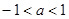 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.