题目内容
3.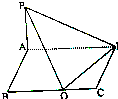 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.(1)使得∠PED=90°
(2)使∠PED为锐角.证明你的结论.
分析 (1)首先当AB≤$\frac{1}{2}$AD时,在边BC上存在点E使∠PED=90°,当AB>$\frac{1}{2}$AD时,在边BC上不存在点E使∠PED=90°.进一步利用直径所对的圆周角为90°得到结论.
(2)利用线面垂直与线线垂直之间的转化得到结论.
解答 解:①当AB≤$\frac{1}{2}$AD时,在边BC上存在点E使∠PED=90°,
当AB>$\frac{1}{2}$AD时,在边BC上不存在点E使∠PED=90°.
证明:当AB≤$\frac{1}{2}$AD时,在边BC上存在点E使∠PED=90°,当AB>$\frac{1}{2}$AD时,在边BC上不存在点E使
∠PED=90°.因为以AD为直径的圆与BC无交点.
②连接BD,做AF⊥BD,垂足为F,连接PF,
由于PA⊥平面ABCD,又△ABD为直角三角形,
所以,F在BD上,
所以:∠PBF为锐角.
进一步得到:∠PED为锐角.
点评 本题考查的知识要点:点的存在性问题,线面垂直与线线垂直之间的转换.

练习册系列答案
相关题目
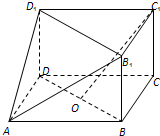 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.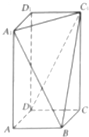 在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.
在长方形ABCD-A1B1C1D1中,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体,若AB=BC=2,且这个几何体的体积为$\frac{40}{3}$.