题目内容
10．化简：（1）$\overrightarrow{AB}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$；
（2）（$\overrightarrow{MA}$+$\overrightarrow{BN}$）+（$\overrightarrow{AC}$+$\overrightarrow{CB}$）；
（3）$\overrightarrow{AB}$+（$\overrightarrow{BD}$+$\overrightarrow{CA}$）+$\overrightarrow{DC}$．
分析 根据向量加法满足交换律及结合律直接计算即可．
解答 解：（1）$\overrightarrow{AB}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{AC}+\overrightarrow{CD}$=$\overrightarrow{AD}$；
（2）（$\overrightarrow{MA}$+$\overrightarrow{BN}$）+（$\overrightarrow{AC}$+$\overrightarrow{CB}$）=$（\overrightarrow{MA}+\overrightarrow{AC}）+（\overrightarrow{CB}+\overrightarrow{BN}）$=$\overrightarrow{MC}+\overrightarrow{CN}$=$\overrightarrow{MN}$；
（3）$\overrightarrow{AB}$+（$\overrightarrow{BD}$+$\overrightarrow{CA}$）+$\overrightarrow{DC}$=$（\overrightarrow{AB}+\overrightarrow{BD}）+（\overrightarrow{DC}+\overrightarrow{CA}）$=$\overrightarrow{AD}+\overrightarrow{DA}$=$\overrightarrow{0}$．
点评 本题考查向量的计算，根据向量加法的交换律和结合律是解题的关键，属基础题．
| A． | $\frac{1}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
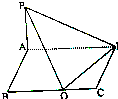在四棱锥P-ABCD中，侧棱PA⊥底面ABCD，底面ABCD是矩形，问底面的边BC上是否存在点E．