Question

8．作图验证：
（1）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）+\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）=\overrightarrow{a}$
（2）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）-\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）=\overrightarrow{b}$．

Answer 1

分析 根据向量的三角形法则，画图验证即．

解答 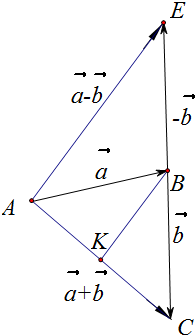证明：如图以A点为起点，作$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}=\overrightarrow{b}$，$\overrightarrow{BE}=-\overrightarrow{b}$，
根据三角形法则，得$\overrightarrow{AE}=\overrightarrow{a}-\overrightarrow{b}$，$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$．
取AC中点K，连结BK，显然BK为△ACE的中位线．
（1）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）+\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）$
=$\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AE}$
=$\overrightarrow{AK}+\overrightarrow{KB}$
=$\overrightarrow{AB}$
=$\overrightarrow{a}$；
（2）$\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）-\frac{1}{2}（\overrightarrow{a}-\overrightarrow{b}）$
=$\frac{1}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AE}$
=$\overrightarrow{KC}-\overrightarrow{KB}$
=$\overrightarrow{KC}+\overrightarrow{BK}$
=$\overrightarrow{BC}$
=$\overrightarrow{b}$．

点评 本题考查向量的三角形法则，属基础题．