题目内容
12.在一台小型的晚会上有歌曲、戏曲、魔术、小品、相声、舞蹈、杂技7个表演节目,其中歌曲节目必须放在最后,且魔术节目不能和相声节目相邻,也不能和小品节目相邻,则不同的表演顺序的种数为( )| A. | 216 | B. | 72 | C. | 144 | D. | 288 |
分析 利用间接法,除歌曲外,先排列没有限制的排列,再排除魔术节目和相声节目相邻或和小品节目相邻的,还要加上魔术节目既和相声节目相邻且和小品节目相邻的,问题得以解决.
解答 解:利用间接法,除歌曲外,没有限制的排列有${A}_{6}^{6}$,再排除魔术节目和相声节目相邻或和小品节目相邻的有2${A}_{2}^{2}•{A}_{5}^{5}$,还要加上魔术节目既和相声节目相邻且和小品节目相邻的有${A}_{2}^{2}•{A}_{4}^{4}$,故不同的表演顺序的种数为${A}_{6}^{6}$-2${A}_{2}^{2}•{A}_{5}^{5}$+${A}_{2}^{2}•{A}_{4}^{4}$=288种,
故选:D.
点评 本题考查计数原理的应用,考查学生分析解决问题的能力,比较基础

练习册系列答案
相关题目
2.函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )


| A. | a>1,b>0 | B. | a>1,b<0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
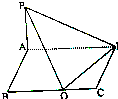 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E. 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.