题目内容
已知函数y=f(x)不恒为0,且对于任意x、y∈R,都有f(x+y)=f(x)+f(y),求证:y=f(x)是奇函数.
证明: 在f(x+y)=f(x)+f(y)中,
令y=-x,得f(0)=f(x)+f(-x),
令x=y=0,则f(0)=f(0)+f(0),所以f(0)=0.
所以f(x)+f(-x)=0,
即f(-x)=-f(x),
所以y=f(x)是奇函数.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ,
, ,
, ,则
,则 B.
B.  C.
C.  D.
D. 
 ,那么2α-
,那么2α- 的取值范围是( )
的取值范围是( )
 在区间[2,4]上的最大值为________,最小值为________.
在区间[2,4]上的最大值为________,最小值为________. 是(-∞,+∞)上的减函数,则实数a的取值范围是( )
是(-∞,+∞)上的减函数,则实数a的取值范围是( ) 使函数值为5的x的值是( )
使函数值为5的x的值是( )
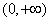 ,且满足f(2)=1,f(xy)=f(x)+f(y).
,且满足f(2)=1,f(xy)=f(x)+f(y).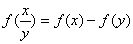
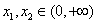 时都有
时都有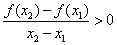 .若
.若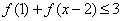 成立,求
成立,求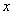 的取值范围
的取值范围