题目内容
12.如果∠A为△ABC的内角,那么“∠A=30°”是“cosA=$\frac{\sqrt{3}}{2}$”的充分不必要条件吗?分析 在△ABC中,由∠A=30°?cosA=$\frac{\sqrt{3}}{2}$,可得“∠A=30°”是“cosA=$\frac{\sqrt{3}}{2}$”的充分必要条件.
解答 解:∠A为△ABC的内角,那么,若∠A=30°,则cosA=$\frac{\sqrt{3}}{2}$,
反之,由cosA=$\frac{\sqrt{3}}{2}$,可得∠A=30°,
∴如果∠A为△ABC的内角,那么“∠A=30°”是“cosA=$\frac{\sqrt{3}}{2}$”的充分必要条件.故不是充分不必要条件.
点评 本题考查充分必要条件的判定方法,考查了三角形中角的三角函数值的求法,是基础题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x(0<x<2)}\\{-{x}^{2}+8x-15(x≥2)}\end{array}\right.$,g(x)=kx-2,若方程f(x)=g(x)有三个根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (-2$\sqrt{13}$+8,1) | D. | ($\frac{1}{2}$,-2$\sqrt{13}$+8) |
7.已知f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{{a}^{x}+b,x≤0}\end{array}\right.$,且f(0)=2,f(-1)=3,则f(f(-3))=( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
1.点A在z轴上,它到点(2$\sqrt{2}$,$\sqrt{5}$,1)的距离是$\sqrt{13}$,则点A的坐标是( )
| A. | (0,0,-1) | B. | (0,1,1) | C. | (0,0,1) | D. | (0,0,13) |
2.已知集合A={(x,y)|y=x2+1},B={y|y=x2+1},则下列关系正确的是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | A∩B=∅ |
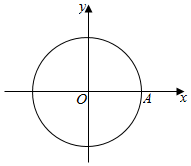 如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.
如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.