题目内容
已知函数f(x)＝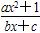
(a，b，c∈Z)是奇函数，又f(1)＝2，f(2)<3，求a，b，c的值．
由f(－x)＝－f(x)，得－bx＋c＝－(bx＋c)，
∴c＝0.
又f(1)＝2，得a＋1＝2b，
而f(2)<3，得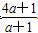
<3，解得－1<a<2，
又a∈Z，∴a＝0或a＝1.
若a＝0，则b＝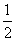
∉Z，应舍去；若a＝1，则b＝1∈Z，
∴a＝1，b＝1，c＝0.
练习册系列答案
阅读快车系列答案
相关题目
)＝0，则不等式f(log4x)>0的解集是________．
阅读快车系列答案题目内容
已知函数f(x)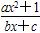＝ (a，b，c∈Z)是奇函数，又f(1)＝2，f(2)<3，求a，b，c的值．
由f(－x)＝－f(x)，得－bx＋c＝－(bx＋c)，
∴c＝0.
又f(1)＝2，得a＋1＝2b，
而f(2)<3，得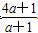<3，解得－1<a<2，
又a∈Z，∴a＝0或a＝1.
若a＝0，则b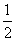＝∉Z，应舍去；若a＝1，则b＝1∈Z，
∴a＝1，b＝1，c＝0.
阅读快车系列答案
，x∈R D．y＝x3＋1，x∈R