Question

【题目】已知数列{an}的各项均为正数，a1=1，前n项和为Sn ， 且an+12﹣nλ2﹣1=2λSn ， λ为正常数．
（1）求数列{an}的通项公式；
（2）记bn= ，Cn= + （k，n∈N*，k≥2n+2）． 求证：
①bn＜bn+1；
②Cn＞Cn+1 ．

Answer 1

【答案】
（1）解：∵a2n+1﹣nλ2﹣1=2λSn，λ为正常数．∴n≥2时， ﹣（n﹣1）λ2﹣1=2λSn﹣1．

∴a2n+1﹣nλ2﹣ +（n﹣1）λ2=2λan．化为：an+1﹣an=λ．

n=1时， ﹣1=2λ，解得a2=λ+1，因此a2﹣a1=λ．

∴数列{an}是等差数列，公差为λ．

∴an=1+λ（n﹣1）

（2）证明：①由（1）可得：Sn= ．

∴bn= = = ．

bn+1﹣bn= = ＞0．

∴bn+1＞bn．

②∵Cn= + ，（k，n∈N*，k≥2n+2）．

∴Cn+1﹣Cn= ﹣ ﹣

= +

= ﹣ ．

∵k≥2n+2，∴n+1＜k﹣n，n＜k﹣n﹣1．

由an＞0，∴0＜Sn＜Sk﹣n﹣1，∴ ．

又0＜bn+1＜bk﹣n，∴ ＜ ，

∴Cn+1﹣Cn＜0．∴Cn＞Cn+1

【解析】（1）a2n+1﹣nλ2﹣1=2λSn ， λ为正常数．可得：n≥2时， ﹣（n﹣1）λ2﹣1=2λSn﹣1 ． 相减化为：an+1﹣an=λ．n=1时， ﹣1=2λ，解得a2=λ+1，因此a2﹣a1=λ．利用等差数列的通项公式可得：an=1+λ（n﹣1）．（2）①由（1）可得：Sn= ．可得bn= = ，作差bn+1﹣bn ， 化简即可得出．②Cn= + ，（k，n∈N*，k≥2n+2）．作差Cn+1﹣Cn= ﹣ ﹣ = ﹣ ．利用其单调性即可得出．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系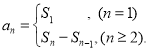；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．