题目内容
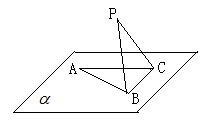
如图,在底面为平行四边形的四棱锥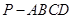 中,
中,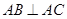 ,
,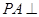 平面
平面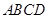 ,且
,且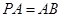 ,点
,点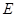 是
是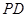 的中点.
的中点.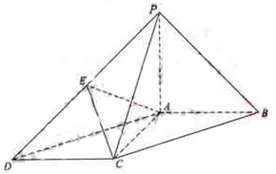
(1)求证: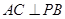 ;
;
(2)求证: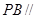 平面
平面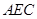 ;
;
(3)求二面角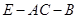 的大小.
的大小.
(1)见解析(2)见解析(3)135°
解析试题分析:(1)利用三垂线定理可证;(2)直线与平面平行的判定定理(Ⅲ)证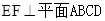 ,进而找出二面角的平面角
,进而找出二面角的平面角
试题解析:(1)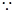
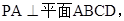
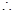 AB是PB在平面ABCD上的射影,
AB是PB在平面ABCD上的射影,
又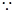 AB
AB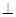 AC,AC
AC,AC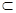 平面ABCD,
平面ABCD,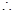 AC
AC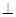 PB.
PB.
(2)连接BD,与AC相交与O,连接EO,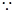 ABCD是平行四边形
ABCD是平行四边形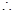 O是BD的中点又E是PD的中点,
O是BD的中点又E是PD的中点,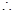 EO
EO PB.又PB
PB.又PB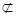 平面AEC,EO
平面AEC,EO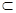 平面AEC,
平面AEC,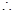 PB
PB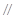 平面AEC,
平面AEC,
(3)如图,取AD的中点F,连EF,FO,则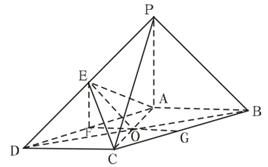
EF是△PAD的中位线, EF
EF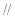 PA又
PA又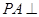 平面
平面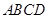 ,
,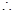
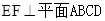
同理FO是△ADC的中位线,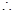 FO
FO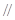 AB
AB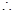 FO^AC,由三垂线定理可知
FO^AC,由三垂线定理可知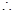 ÐEOF是二面角E-AC-D的平面角.又FO=
ÐEOF是二面角E-AC-D的平面角.又FO= AB=
AB= PA=EF。
PA=EF。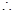 ÐEOF=45°而二面角
ÐEOF=45°而二面角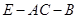 与二面角E-AC-D互补,
与二面角E-AC-D互补,
故所求二面角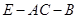 的大小为135°.
的大小为135°.
考点:利用三垂线定理可证;直线与平面平行的判定定理;出二面角的平面角

练习册系列答案
相关题目
 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点. 平面
平面 ;
; 平面
平面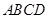 ;
; 为正方体
为正方体 的点
的点 的个数,并说明理由.
的个数,并说明理由.
 中,
中, ,G是
,G是 上的动点。
上的动点。

 ;
; 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;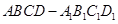 中,已知
中,已知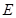 为棱
为棱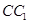 上的动点.
上的动点.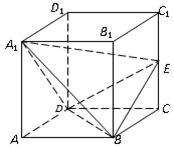
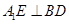 ;
;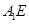 与平面
与平面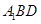 所成角的正弦值.
所成角的正弦值. 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, .
.
 平面
平面 ;
; 平面
平面 .
.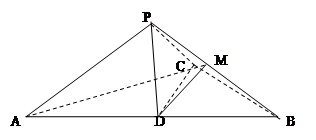 .
.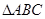 在平面
在平面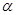 内,
内,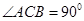 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面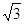 ,
,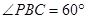
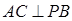
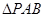 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值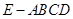 ,底面
,底面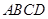 是矩形,平面
是矩形,平面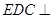 底面
底面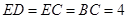 ,
,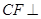 平面
平面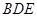 ,且点
,且点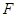 在
在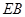 上.
上.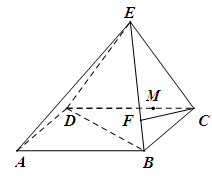
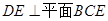 ;
;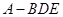 的体积;
的体积;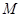 在线段
在线段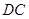 上,且满足
上,且满足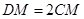 ,试在线段
,试在线段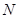 ,使得
,使得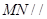 平面
平面 .
.