命题p:?x∈R.函数$f(x)=2{cos^2}x+\sqrt{3}sin2x≤3$的否定为?x0∈R.函数f(x0)=2cos2x0+$\sqrt{3}$sin2x0＞3．题目和参考答案——青夏教育精英家教网—

题目内容

12．命题p：?x∈R，函数$f（x）=2{cos^2}x+\sqrt{3}sin2x≤3$的否定为?x₀∈R，函数f（x₀）=2cos²x₀+$\sqrt{3}$sin2x₀＞3．

分析根据全称命题的否定是特称命题进行判断即可．

解答解：全称命题的否定是特称命题，即为?x₀∈R，函数f（x₀）=2cos²x₀+$\sqrt{3}$sin2x₀＞3，
故答案为：?x₀∈R，函数f（x₀）=2cos²x₀+$\sqrt{3}$sin2x₀＞3，

点评本题主要考查含有量词的命题的否定，比较基础．

练习册系列答案

3．某种定点投篮游戏的规则如下：每人投篮10次，如果某同学某次没有投进，则罚该同学做俯卧撑2个．现有一同学参加该游戏，已知该同学在该点投篮的命中率为0.6，设该同学参加本次比赛被罚做俯卧撑的总个数记为X，则X的数学期望为（　　）

20．

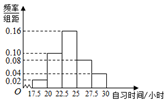某中学调查200名学生每周晚自习时间（单位，小时），制成了如图所示频率分布直方图，其中自习时间的范围为[17.5，30]，根据直方图，这200名学生每周自习时间不少于22.5小时的人数是140．

7．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上一点P到左焦点的距离为5，则点P到右焦点的距离为（　　）

17．已知椭圆$T：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F₁，F₂，动点P在椭圆上运动，|PF₁|•|PF₂|的最大值为25，且点P到F₁的距离的最小值为1．
（1）求椭圆T的方程；
（2）直线l与椭圆T有且仅有一个交点A，且l切圆M：x²+y²=R²（其中（3＜R＜5））于点B，求A、B两点间的距离|AB|的最大值；
（3）当过点C（10，1）的动直线与椭圆T相交于两不同点G、H时，在线段GH上取一点D，满足$|{\overrightarrow{GC}}|•|{\overrightarrow{HD}}|=|{\overrightarrow{GD}}|•|{\overrightarrow{CH}}|$，求证：点D在定直线上．

4．执行下面的程序框图，若输入的N是5，那么输出的S=-46．

1．若直线AB的方程为$\sqrt{3}$x+y-7=0，则直线AB的倾斜角是（　　）

2．

一种饮料每箱装有6听，经检测，某箱中每听的容量（单位：ml）如以下茎叶图所示．
（Ⅰ）求这箱饮料的平均容量和容量的中位数；
（Ⅱ）如果从这箱饮料中随机取出2听饮用，求取到的2听饮料中至少有1听的容量为250ml的概率．

试题分类